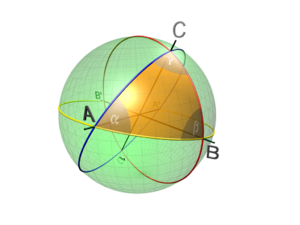
- Gran círculo
-
- Para otros usos de círculo, véase Círculo (desambiguación)
Un gran círculo divide la esfera en dos hemisferios iguales.
El gran círculo, denominado también círculo mayor o círculo máximo, es el círculo resultante de una sección realizada a una esfera mediante un plano que pase por su centro y la divida en dos hemisferios idénticos; la sección circular obtenida tiene el mismo diámetro que la esfera.
La distancia más corta entre dos puntos de la superficie de una esfera siempre es el arco de círculo máximo que los une.
Contenido
Aplicaciones de círculos máximos
Geometría riemanniana
En la geometría riemanniana este concepto sirve para ilustrar como hay espacios donde hay puntos (los antipodales) que admiten más de una geodésica contrastando lo que sucede en espacios euclídeos donde por cualquiera dos puntos arbitrarios sólo pasa una única geodésica.
Triángulos esféricos
Aplicación de círculos máximos en triángulo esférico.Si tres puntos de la superficie esférica son unidos por arcos de círculo máximo menores a 180º, la figura obtenida se denomina triángulo esférico. Los lados del polígono así formado se expresan por conveniencia como ángulos cuyo vértice es el centro de la esfera y no por su longitud. Este arco medido en radianes y multiplicado por el radio de la esfera es la longitud del arco. En un triángulo esférico los ángulos cumplen que: 180° <
+ 
+ 
< 540°Geografía y cartografía
En geografía y cartografía, los círculos máximos que pasan por los polos determinan las líneas de longitud (meridianos). En la latitud, en cambio, existe sólo un círculo máximo: el ecuador terrestre. Las demás latitudes están determinadas por círculos menores paralelos al ecuador (paralelos).
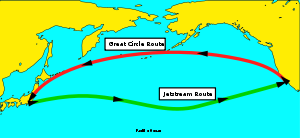La trayectoria del gran círculo de una ruta aérea (línea roja)
La trayectoria siguiendo una corriente en chorro (línea verde).Véase también
Enlaces externos
- Weisstein, Eric W. Great Circle From MathWorld. (en inglés)
- Gran círculo: calculadora de distancias (en inglés)
- Um simulador de rotas ortodrómicas (en portugués)
- Instrumento para traçar rotas ortodrómicas (en portugués)
- Cartografía y distancia de Herramientas
Categorías:- Términos de geografía
- Geometría elemental
- Trigonometría
Wikimedia foundation. 2010.
