- Coeficiente de Gini
-
Mapa esquemático de países según su nivel de igualdad de ingreso, de acuerdo al coeficiente de Gini. < 0,25 0,25 ↔ 0,29 0,30 ↔ 0,34 0,35 ↔ 0,39 0,40 ↔ 0,44 0,45 ↔ 0,49 0,50 ↔ 0,54 0,55 ↔ 0,59 ≥ 0,60 Sin datos
El Coeficiente de Gini es una medida de la desigualdad ideada por el estadístico italiano Corrado Gini.Normalmente se utiliza para medir la desigualdad en los ingresos, pero puede utilizarse para medir cualquier forma de distribución desigual.
El coeficiente de Gini es un número entre 0 y 1, en donde 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos) y donde el valor 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno).
El índice de Gini es el coeficiente de Gini expresado en porcentaje, y es igual al coeficiente de Gini multiplicado por 100.
Aunque el coeficiente de Gini se utiliza sobre todo para medir la desigualdad en los ingresos, también puede utilizarse para medir la desigualdad en la riqueza. Este uso requiere que nadie disponga de una riqueza neta negativa.
Contenido
Definición
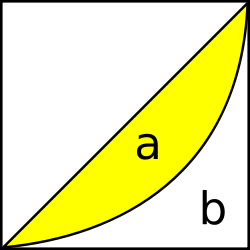
Diagrama que muestra el área a comprendida entre la curva de Lorenz y la bisectriz del cuadrado, dicha área es proporcional al coeficiente de Gini.El coeficiente de Gini se calcula como una razón de las áreas en el diagrama de la curva de Lorenz. Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b).
Esta razón se expresa como porcentaje o como equivalente numérico de ese porcentaje, que es siempre un número entre 0 y 1. El coeficiente de Gini se calcula a menudo con la Fórmula de Brown, que es más práctica:
Donde:
- G: Coeficiente de Gini
- X: Proporción acumulada de la variable población
- Y: Proporción acumulada de la variable ingresos
De forma resumida, la Curva de Lorenz es una gráfica de concentración acumulada de la distribución de la riqueza superpuesta a la curva de la distribución de frecuencias de los individuos que la poseen, y su expresión en porcentajes es el índice de Gini.
Propiedades
- Todas las curvas de Lorenz pasan por los puntos (0,0) y (1,1). Si dos curvas de Lorenz no se cortan fuera de esos dos puntos, es posible comparar la desigualdad que representan sin necesidad de calcular el índice de Gini. En el caso general, un mayor índice de Gini significa una mayor desigualdad.
- Para determinar el área entre la curva de Lorenz y la línea de perfecta equidad, lo ideal es calcular una integral definida, pero a veces no se conoce la definición explícita de la curva de Lorenz, por lo que es interesante utilizar otras fórmulas con un número finito de sumandos.
- Las propiedades del índice de Gini son comparables con las del cuadrado del coeficiente de variación.[1]
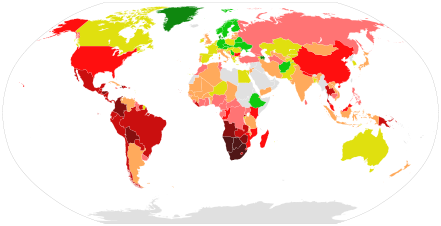
El índice de Gini en varios países
Algunos valores del informe de 2007 eran los siguientes:[2]
- Namibia: 70.7 (peor distribución)
- Sudáfrica: 65.0
- Lesoto: 63.2
- Botsuana: 63.0
- Sierra Leona: 62.9
- República Centroafricana: 61.3
- Bolivia: 59.2
- Haiti: 59.2
- Paraguay: 58.4
- Zimbabue: 56.8
- Panamá: 56.1
- Brasil: 55.6*
- Guatemala: 55.1
- Chile: 54.3*
- Colombia: 53.8
- Honduras: 53.8
- Hong Kong: 53.3
- El Salvador:52.4
- Singapur: 52.2
- Perú: 52.0
- México: 50.9
- Zambia: 50.8
- Argentina: 48.3
- Ecuador: 46.0
- Uruguay: 45.2
- Estados Unidos:45.0
- Nicaragua: 43.1
- Costa Rica: 42.1
- Venezuela: 41.2
- Portugal: 38.5
- Italia: 33.0
- España: 32.0
- Hungría: 28.0
- Francia: 28.0
- Alemania: 28.0
- Noruega: 28.0
- Albania: 26.7
- Finlandia: 26.0
- Dinamarca: 24.0
- Suecia: 23.0 (mejor distribución)
Referencias
- ↑ Gonzalez, Luis; et al. (2010). «The Similarity between the Square of the Coeficient of Variation and the Gini Index of a General Random Variable». Revista de Métodos Cuantitativos para la Economía y la Empresa 10: p. 5-18. ISSN 1886-516X. http://www.upo.es/RevMetCuant/art.php?id=40.
- ↑ Gini Index by Country, recogidos en Nation Master
Bibliografía
- Fedriani, E.M.; Martín, A.M. (2009). Distribución personal y funcional de la renta. Cap. en: José Vallés Ferrer, ed. Economía Española (2a edición). McGraw-Hill/Interamericana de España S.A.U., pp. 331-345. Madrid. ISBN: 978-84-481-6806-3.
- Medina, F. (2001). Consideraciones sobre el índice de Gini para medir la concentración del ingreso. CEPAL, Santiago de Chile. ISBN 92-1-321793-5 (documento PDF)
- René Fernández Montt, Concentración de la Propiedad en Latinoamérica, 2011
Véase también
- Desigualdad de ingreso
- Desigualdad social
- Distribución de la renta
- Eficiencia distributiva
- Lista de países por igualdad de ingreso
- Índice de Atkinson
- Índice de Dalton
- Índice de desarrollo humano.
- Índice de Theil
Enlaces externos
- La distribución de la renta, la curva de Lorenz y el índice de Gini
- Calculadora (en inglés): http://www.poorcity.richcity.org/calculator
- Hoja de cálculo (en inglés)
- Gráfico que muestra la distribución de los paises en función de su riqueza ( en renta per cápita en dólares internacionales PPA ) y su grado de igualdad social: http://img69.imageshack.us/my.php?image=gdppercapitapppversusinsd6.png
- (en inglés) A complete handhout about the Lorenz curve including various applications, including an Excel spreadsheet graphing Lorenz curves and calculating Gini coefficients as well as coefficients of variation.
- Hoja de cálculo Excel que calcula el Índice de Gini, el Índice de Theil, la Redundancia, la Redundancia relativa, y representa la Curva de Lorenz: http://trucosexcel.blogspot.com/2011/05/indice-de-gini.html
Categorías:- Listas e índices económicos
- Indicadores sociales
- Indicadores económicos
- Investigación social
Wikimedia foundation. 2010.
