- Teorema de los cuatro colores
-
Ejemplo de mapa coloreado con cuatro colores.
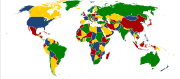
Mapa del mundo coloreado de verde, amarillo, azul y rojo.En teoría de grafos, el teorema de cuatro colores es un teorema sobre la coloración de grafos que establece lo siguiente:
Dado cualquier mapa geográfico con regiones continuas, éste puede ser coloreado con cuatro colores diferentes, de forma que no queden regiones adyacentes (es decir, regiones que compartan no sólo un punto, sino todo un segmento de borde en común) con el mismo color.
No es posible colorear cualquier mapa en estas condiciones utilizando sólo tres colores. En cambio, sí es posible hacerlo considerando cinco colores.[1]
El problema de los cuatro colores fue planteado por primera vez por Francis Guthrie en 1852 y resuelto positivamente en 1976 por Kenneth Appel y Wolfgang Haken.
Contenido
La polémica demostración
El teorema de cuatro colores ha sido demostrado con la ayuda de un ordenador. La prueba sin embargo, no es aceptada por todos los matemáticos dado que sería impracticable por su gran cantidad de detalles que una persona se vería imposibilitada de verificar manualmente. Sólo queda aceptar la exactitud del programa, del compilador y del computador en el cual se ejecutó la prueba.
Otro aspecto de la prueba, que puede ser considerado negativo, es su falta de elegancia. Una crítica sin mucho sentido que habla sobre la elegancia de la prueba, comentada en la época de su publicación, dice:
En la actualidad ya se realizó otra demostración, pero también haciendo uso de cálculos en la computadora, lo cual verifica la prueba original, pero queda la interrogante de una prueba que se pueda efectuar con lápiz y papel.
Generalizaciones
Uniendo las flechas simples y las flechas dobles, se obtiene un toro con siete regiones colindantes, con lo que son necesarios siete colores.
Esta construcción muestra un toro dividido en el máximo de siete regiones, cada una de las cuales toca a las otras.Se ha estudiado también el problema de colorear otras superficies que no sean equivalentes a un plano. Para superficies cerradas (orientables o no orientables) con género positivo, el número máximo de colores p que se necesitan depende de la característica de Euler χ, dados por la siguiente fórmula:
donde los paréntesis externos determinan la función piso.
Alternativamente, para una superficie orientable, la fórmula puede ser dada en términos del género de la superficie, g:
-
(Weisstein).
Esta fórmula, conocida como conjetura de Heawood, fue conjeturada por P. J. Heawood en 1890 y demostrada para los casos de superficies orientables (y no orientables) no acotadas por Gerhard Ringel y J. T. W. Youngs en 1968. La única excepción a la fórmula es la Botella de Klein, que tiene una característica de Euler 0 (de ahí la fórmula da p=7) y requiere 6 colores, como lo demostró P. Franklin en 1934 (Weisstein). (Una Banda de Möbius, cuya característica de Euler χ = 0, también requiere 6 colores, pero en este caso la fórmula no es aplicable, puesto que es una superficie acotada. (Weisstein))
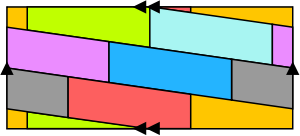
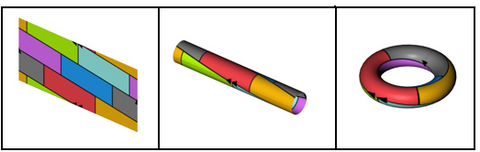
El toro tiene una característica de Euler χ = 0 (y género g = 1) y por lo tanto p = 7, de manera que no más de 7 colores son requeridos para colorear cualquier mapa sobre un toro. El Poliedro de Szilassi es otro ejemplo que requiere 7 colores.
No hay extensión obvia del problema de coloreo de regiones de sólidos tridimensionales. Usando un conjunto de n varillas flexibles, uno puede hacer que cada varilla toque a cada una de las otras. El conjunto luego requerirá n colores, o n+1 si se considera que el espacio vacío también toca cada varilla. Para el número n puede tomarse un entero tan grande como se quiera. tales ejemplos fueron propuestos por Fredrick Gurthrie en 1880. (Wilson, 2002)
Referencias
- ↑ Thomas, Robin (1998), «An Update on the Four-Color Theorem», Notices of the American Mathematical Society 45 (7): 848–859, http://www.ams.org/notices/199807/thomas.pdf
- ↑ Mathematics, Microsoft Encarta Online Encyclopedia, Microsoft Corporation, 2007. (en inglés)
- Gonthier, Georges (2008), «Formal Proof--The Four-Color Theorem», Notices of the American Mathematical Society 55 (11): 1382–1393, http://www.ams.org/notices/200811/tx081101382p.pdf
- Wilson, Robin (2002), Four Colors Suffice, London: Penguin Books, ISBN 0-691-11533-8
- Weisstein, Eric W. «Four-Color Theorem» (en inglés). MathWorld. Wolfram Research.
- Weisstein, Eric W. «Map coloring» (en inglés). MathWorld. Wolfram Research.
Enlaces externos
- Teorema de los cuatro colores Artículo divulgativo sobre la historia del problema de los cuatro colores.
Categorías:- Mapas
- Teoremas de teoría de grafos
- Coloreo de grafos
Wikimedia foundation. 2010.
