La demostración automática de teoremas (de siglas ATP, por el término en inglés: Automated theorem proving) que también puede ser denominada Deducción automatizada, es actualmente el subcampo más desarrollado del razonamiento automático, y se encarga de la demostración de teoremas matemáticos mediante programas de ordenador.

Contenido 1 Definición 2 El problema de deducir un teorema 3 Problemas relacionados 4 Usos industriales 5 Demostración de teoremas de primer orden 6 Software libre 6.1 Software propietario incluyendo los no comerciales 7 Referencias

Definición

Las técnicas de demostración automática de teoremas consisten en aplicar métodos computacionales para demostrar teoremas. Es decir, demostración de teoremas con un ordenador. Estas técnicas son especialmente viables como herramienta para demostrar teoremas de geometría plana.

En líneas generales, el procedimiento es el siguiente:

1. El teorema a demostrar se traduce en términos algebraicos: tanto las hipótesis como la tesis se expresan como condiciones del tipo 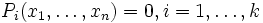y 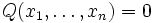respectivamente.
2. La veracidad del teorema es entonces equivalente a que 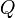esté en el ideal generado por 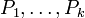(lo que equivale a que la anulación de 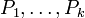en un punto implique la anulación de 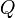en ese punto).
3. El problema de pertenencia de un polinomio a un ideal es un problema clásico en álgebra computacional; una técnica habitual de resolución de este problema es el cálculo de una base de Gröbner adecuada.

Este método de demostración tiene el inconveniente de que la complejidad computacional del problema de pertenencia es elevada.

El problema de deducir un teorema

Dependiendo de la lógica subyacente, el problema de decidir sobre si un teorema es válido o no, varía desde ser una tarea trivial a imposible. Para el caso frecuente de la lógica proposicional, el problema es deducible pero NP-completo, y por lo tanto se cree que solamente existen algoritmos de tiempo exponencial para las tareas generales de la prueba. Para un cálculo de predicado de primer orden, que no posee ningún axioma apropiado el Teorema de la completitud de Gödel indica que los teoremas son exactamente las fórmulas bien formadas lógicamente válidas, así que la identificación de teoremas es recurrentemente enumerable, es decir que con recursos ilimitados eventualmente todo teorema válido pueden ser demostrado. Las proposiciones inválidas, es decir las fórmulas que no son exigidas por una teoría dada, no siempre pueden ser reconocidas. Además, una teoría formal consistente que contiene la teoría de primer orden de los números naturales (o sea que tiene ciertos axiomas apropiados), por el teorema del estado incompleto de Gödel, contiene una proposición verdadera que no puede ser demostrada, en este caso un "demostrador" del teorema que intenta demostrar tal proposición concluye en un punto indefinido.

En estos casos, un demostrador de primer orden del teorema puede no poder terminar mientras que busca una demostración. A pesar de estos límites teóricos, los demostradores prácticos del teorema pueden solucionar muchos problemas difíciles con estas lógicas.

Problemas relacionados

Un problema relacionado pero más simple es la verificación de la demostración, donde se certifica la validez de una demostración existente de un teorema. Para poder hacer esto, se requiere generalmente que cada paso individual de la demostración pueda ser verificado por una función recurrente primitiva o programa, y por lo tanto el problema es siempre decidible.

Los demostradores interactivos de teorema requieren de un usuario humano para darle pistas al sistema. Dependiendo del grado de automatización, el demostrador puede ser reducido a un probador de la demostración, con el usuario proporcionando la demostración de una manera formal, o tareas importantes de la demostración se pueden realizar automáticamente. Los demostradores interactivos se utilizan para numerosas tareas, en algunos casos sistemas completamente automáticos han logrado demostrar una cantidad de teoremas interesantes y difíciles, incluyendo algunos que han eludido a los matemáticos humanos durante mucho tiempo. Sin embargo estos éxitos son esporádicos, y el trabajo sobre problemas difíciles requiere por lo general de un usuario ágil y con conocimiento.

A veces se distingue entre demostrar un teorema y otras técnicas, se considera que un proceso demuestra un teorema si consiste de una demostración tradicional, comenzando con axiomas y produciendo nuevos pasos de la inferencia utilizando reglas de inferencia. Otras técnica es la "comprobación del modelo", que es equivalente a la enumeración por medio de la fuerza bruta de muchos estados posibles (aunque como la puesta en práctica real de probadores del modelo requiere mucha inteligencia, es algo excesivo decir que el método solo requiere de fuerza bruta). Ecxisten sistemas demostradores de teoremas híbridos que utilizan prueba de modelo a manera de regla de inferencia. Existen también programas que fueron escritos para demostrar un teorema particular, con una demostración (por lo general informal) consistente en que si el programa termina con un cierto valor el teorema es verdadero. Un ejemplo de ello es la demostración automática del Teorema de los cuatro colores, que fue motivo de gran controversia ya que fue la primera demostración matemática que fue imposible de comprobar por un humano debido a la enorme tamaño de los cálculos realizados por el programa (tales demostraciones se denominan demostraciones no verificables). Otro ejemplo es la demostración que en el juego de Unir Cuatro gana el primer jugador.

Usos industriales

La demostración automática de teoremas se utiliza principalmente en el diseño y la verificación de circuitos integrados, por la industria electrónica. Desde el bug FDIV del Pentium, la sofisticada y complicada unidad de punto flotante de los microprocesadores modernos se han diseñado utilizando pasos de escrutinio adicional. En los más modernos procesadores de AMD, Intel, y otros, se ha utilizado el demostrador automatizado de teoremas para verificar que las operaciones matemáticas de división y otras han sido diseñadas correctamente. Una de las vías para demostrar teoremas es el principio de resolución, que funciona nada más y nada menos que como una regla de inferencia más y basado principalmente en la regla más vieja (Modus Ponens). Este método consiste en demostrar un conjunto de axiomas mediante la refutación de los mismos y en ocasiones contando con premisas.

Demostración de teoremas de primer orden

La denominada "demostración de teoremas de primer orden" puede ser reducida a un cálculo proposicional con "términos" (constantes, nombres de funciones, y variables libres) agregados, lo que hace imposible expresar una inducción matemática.^{[notes 1]} . Por lo tanto no debe ser confundida con una teoría de primer orden de las metamatemáticas, ya que los cuantificadores han sido eliminados, si bien es posible emular a los cuantificadores universales reescribiéndolos como variables libres.

La demostración de teoremas de primer orden es uno de los campos más maduros de la demostración automática de teoremas. La lógica es lo suficientemente expresiva para permitir la formulación de problemas arbitrarios, a menudo de una forma natural e intuitiva. Por otra parte, es aún semi-decible, y se han desarrollado una cierta cantidad de cálculos completos y correctos, permitiendo la creación de sistemas completamente automáticos. Lógicas más expresivas, tales como lógicas de mayor orden y modales, permiten expresar en forma adecuada un conjunto mayor de problemas que la lógica de primer orden, pero los demostradores de problemas se encuentran menos desarrollados para éste tipo de lógicas. La calidad de los sistemas existentes ha sido beneficiada por la existencia de un gran conjunto de ejemplos estandard de comprobación (el TPTP), como también los producidos por la Competición ATP organizada por la CADE (CASC), una competición de sistemas de primer orden que se ocupa de muchas clases de problemas de primer orden.

Algunos sistemas destacados son los siguientes (cada uno de ellos ha ganado por lo menos en una categoría de la competición CASC).

• E es un demostrador de alta performance para lógicas de primer orden, construido a partir de cálculo de ecuaciones puro, ha sido desarrollado principalmente por el grupo de razonamiento automatizado de la Technical University of Munich.
• Otter, desarrollado por el Argonne National Laboratory, es el primer demostrador de teoremas que alcanzó amplia difusión. Está basado en resolución de primer orden y paramodulación. Otter ha sido reemplazado por Prover9, el cual se asemeja a Mace4.
• SETHEO es un sistema de alta performance basado en un modelo de eliminación orientado a objetivos. Es un desarrollo del grupo de razonamiento automatizado de la Technical University of Munich. E y SETHEO han sido combinados (junto con otros sistemas) para formar el sistema demostrador compuesto E-SETHEO.
• Vampire es desarrollado e implementado en la Manchester University por Andrei Voronkov, que trabajara con Alexandre Riazanov. Ganó el "campeonato mundial de los demostradores de teoremas" (la competición de sistemas ATP CADE) en la categoría más prestigiosa CNF (MIX) durante ocho años (1999, 2001 - 2007).
• Waldmeister es un sistema especializado para lógica de primer orden de ecuaciones de unidad. Ganó la categoría UEQ en las competencias CASC durante el período (1997-2006).

Software libre

Software propietario incluyendo los no comerciales

Referencias

Traducción de la wikipedia en idioma inglés

• Chin-Liang Chang; Richard Char-Tung Lee (1973). Symbolic Logic and Mechanical Theorem Proving. Academic Press.
• Loveland, Donald W. (1978). Automated Theorem Proving: A Logical Basis. Fundamental Studies in Computer Science Volume 6. North-Holland Publishing.
• Gallier, Jean H. (1986). Logic for Computer Science: Foundations of Automatic Theorem Proving. Harper & Row Publishers.
• Duffy, David A. (1991). Principles of Automated Theorem Proving. John Wiley & Sons.
• Wos, Larry; Overbeek, Ross; Lusk, Ewing; Boyle, Jim (1992). Automated Reasoning: Introduction and Applications, 2nd edition edición, McGraw-Hill.
• (2001) Alan Robinson and Andrei Voronkov (eds.) (ed.). Handbook of Automated Reasoning Volume I & II. Elsevier and MIT Press.
• Fitting, Melvin (1996). First-Order Logic and Automated Theorem Proving, 2nd edition edición, Springer.

Error en la cita: Existen etiquetas <ref> para un grupo llamado "notes", pero no se encontró una etiqueta <references group="notes"/>