Función compuesta

Función compuesta
g o f, es la aplicación resultante de la aplicación sucesiva de f y de g. En el ejemplo, (g o f)(a)=@.

En matemática, una función compuesta es una función formada por la composición o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante.

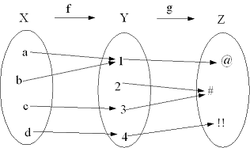
Formalmente, dadas dos funciones f: X → Y y g: Y → Z, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ο f ): X → Z como (g ο f)(x) = g (f(x)), para todos los elementos x de X.

X \to \,\,Y\;\; \to \;\;\,Z
x \mapsto f(x) \mapsto g(f(x))

A g ο f se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.

Ejemplo

Sean las funciones:

f(x) = x^2 \,
g(x) = sin(x) \,

La función compuesta de g y de f que expresamos:

(f \circ g)(x) = f(g(x)) = (sin(x))^2 = sin^2 (x) \,

La interpretación de (f o g) aplicada a la variable x significa que primero tenemos que aplicar g a x, con lo que obtendríamos un valor de paso

z = g(x)=sin(x) \,

y después aplicamos f a z para obtener

y = f(z) = z^2 = sin^2(x) \,

Función bien definida

La función compuesta está bien definida porque cumple con las dos condiciones de existencia y unicidad, propias de toda función:

  1. Condición de existencia: dado x, conocemos (x, f(x)), puesto que conocemos la función f, y dado cualquier elemento y de B conocemos también (y, g(y)), puesto que conocemos la función g. Por tanto, (x, g( f(x)) ) está definido para todo x, y así (g ο f) cumple la condición de existencia.
  2. Condición de unicidad: como f y g son funciones bien definidas, para cada x el valor de f(x) es único, y para cada f(x) también lo es el de g( f(x)).

Propiedades

  • La composición de funciones es asociativa, es decir:

h\circ (g \circ f) = (h\circ g) \circ f

  • La composición de funciones en general no es conmutativa, es decir:

(g \circ f) \neq (f\circ g)

Por ejemplo, dadas las funciones numéricas f(x)=x+1 y g(x)=x², entonces f(g(x))=x²+1, en tanto que g(f(x))=(x+1)².
  • La inversa de la composición de dos funciones es:

(g \circ f)^{-1} = f^{-1} \circ g^{-1}


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Función sigma — Saltar a navegación, búsqueda La Función Sigma o Celeométrica, es la función compuesta de tres variables no colineales. Representa la variación temporal de tres variables (a,b,c), en cuanto {a,b,c} pertenecen al conjunto euclídeo, de Rn, siendo n …   Wikipedia Español

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… …   Wikipedia Español

  • Función continua — En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente… …   Wikipedia Español

  • Función cuantil — En probabilidad la función cuantil de una distribución de probabilidad es la inversa de la función de distribución.[1] Dada una función de distribución continua y estrictamente monótona, , la función cuantil, F −1, devuelve un valor x tal… …   Wikipedia Español

  • Función periódica — La onda periódica más simple: una onda armónica. En este ejemplo, A=1, Ω=1 y θ=0. Las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple: donde …   Wikipedia Español

  • Función iterada — En matemáticas, función iterada es una función que es compuesta consigo misma, en forma repetida, en un proceso llamado iteración. Las funciones iteradas son objeto de profundos estudios en el campo de los fractales y sistemas dinámicos.… …   Wikipedia Español

  • Oración compuesta — Árbol sintáctico, para una oración compuesta (el niño que me saludó me odia) en la que la oración subordinada es una oración de relativo. Se denomina oración compuesta a una oración que tiene más de un sintagma verbal o, dicho de otro modo, a una …   Wikipedia Español

  • Regla de la cadena — Saltar a navegación, búsqueda En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones. Descripción de la …   Wikipedia Español

  • Funciones de parte entera — En matemática, las funciones de parte entera son aquellas funciones: que toman un número real y devuelven un número entero mayor o menor a ese número. Las funciones más conocidas son la función piso[1] y la función techo.[2] …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”