- Funciones de parte entera
-
En matemática, las funciones de parte entera son aquellas funciones:
que toman un número real y devuelven un número entero mayor o menor a ese número. Las funciones más conocidas son la función piso[1] y la función techo.[2]
Contenido
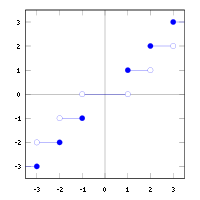
Función techo
La función techo se aplica a un número real x y devuelve el mínimo número entero k no inferior a x:
O de otra forma:
Propiedades
- Para cualquier número real se cumple que
 .
. - El número real x al que se aplica la función techo es un número entero si y sólo si la función techo de x tiene el mismo valor que x.

- La función techo tiene puntos de discontinuidad en los números enteros pero es diferenciable para el resto de puntos.
- La función techo puede expresarse como integral mediante la delta de Dirac y la función característica del conjunto de los enteros:

Ejemplos
Para un número real no entero:
Para un número entero:
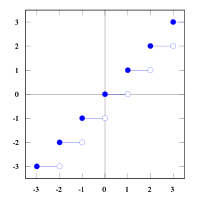
Función piso
La función piso se aplica a un número real x y devuelve el máximo número entero k no superior a x:
Que se puede expresar:
Propiedades
El número real x al que se aplica la función piso es un número entero si y sólo si la función piso de x tiene el mismo valor que x.
Ejemplos
Para un número real no entero:
Para un número entero:
Serie de expansión para la función piso, techo y parte entera
La función piso no es continua, y por lo tanto no tiene un expansión en serie de Taylor; como no es periódica, tampoco tiene una expansión en serie de Fourier. Sin embargo, la función
 , llamada función de parte decimal, fraccionaria o función mantisa, es periódica, y por lo tanto tiene una expansión en serie de Fourier, que es:
, llamada función de parte decimal, fraccionaria o función mantisa, es periódica, y por lo tanto tiene una expansión en serie de Fourier, que es:Usando la expresión
 podemos saber la expansión de la función
podemos saber la expansión de la función  :
:Teniendo en cuenta que:
 , entonces la expansión de serie de la función techo sería:
, entonces la expansión de serie de la función techo sería:Y por último, para la función de parte entera en el lenguaje C, se utilizará la siguiente expresión
 ; entonces quedaría:
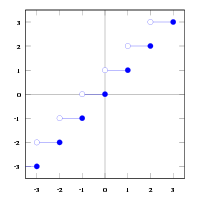
; entonces quedaría:Función parte entera
La función parte entera en el lenguaje de programación C es una función compuesta de la función piso[3] y techo,[4] se define de la siguiente manera:
![\operatorname{int}(x)=[x] = \begin{cases} \mathrm{si \ \ } x\ge 1 \quad & [x]=\lfloor x \rfloor \\
\mathrm{si \ \ } -1< x< 1 \quad & [x]=0 \\
\mathrm{si \ \ } x \le -1 \quad & [x]= \lceil x \rceil
\end{cases}](9/659ff1e3a19ca81430d7fef8ae599526.png)
Se utiliza mediante el operador (int) para truncar el valor de variables del tipo float o double.
Véase también
- Continuidad (matemática)
- Función signo
- Función unitaria de Heaviside
- Representación de números con signo en ordenadores
Notas y Referencias
- ↑ Algunos lenguajes de programación tienen una implementación nativa de la función piso llamada generalmente floor o Floor
- ↑ Algunos lenguajes de programación tienen una implementación nativa de la función techo llamada generalmente ceil o Ceil
- ↑ «C++ reference of
floorfunction». Consultado el 24 de abril de 2011. - ↑ «C++ reference of
ceilfunction». Consultado el 24 de abril de 2011.
Enlaces externos
- Weisstein, Eric W. «Floor Function» (en inglés). MathWorld. Wolfram Research.
- Weisstein, Eric W. «Ceiling Function» (en inglés). MathWorld. Wolfram Research.
- Štefan Porubský, "Integer rounding functions", Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic.
Categoría:- Funciones especiales elementales
Wikimedia foundation. 2010.