Estimador

Saltar a navegación, búsqueda

En estadística, un estimador es un estadístico (esto es, una función de la muestra) usado para estimar un parámetro desconocido de la población. Por ejemplo, si se desea conocer el precio medio de un artículo (el parámetro desconocido) se recogerán observaciones del precio de dicho artículo en diversos establecimientos (la muestra) y la media aritmética de las observaciones puede utilizarse como estimador del precio medio.

Para cada parámetro pueden existir varios estimadores diferentes. En general, escogeremos el estimador que posea mejores propiedades que los restantes, como insesgadez, eficiencia, convergencia y robustez (consistencia).

El valor de un estimador proporciona lo que se denomina en estadística una estimación puntual del valor del parámetro en estudio. En general, se suele preferir realizar una estimación mediante un intervalo, esto es, obtener un intervalo [a,b] dentro del cual se espera esté el valor real del parámetro con un cierto nivel de confianza. Utilizar un intervalo resulta más informativo, al proporcionar información sobre el posible error de estimación, asociado con la amplitud de dicho intervalo. El nivel de confianza es la probabilidad de que a priori el verdadero valor del parámetro quede contenido en el intervalo.

En la práctica, en los intervalos suelen indicarse dando el valor del estimador puntual utilizado como centro del intervalo y un valor que debe sumarse y restarse para obtener el límite superior e inferior, por ejemplo:

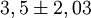$3,5 \pm 2,03\;$ equivale a $[3,5-2,03\,;\,3,5+2,03]=[1,47\,;\,5,53]$

Contenido

1 Propiedades de los estimadores

Propiedades de los estimadores

Sesgo

Se denomina sesgo de un estimador a la diferencia entre la esperanza (o valor esperado) del estimador y el verdadero valor del parámetro a estimar. Es deseable que un estimador sea insesgado o centrado, es decir, que su sesgo sea nulo por ser su esperanza igual al parámetro que se desea estimar.

Por ejemplo, si se desea estimar la media de una población, la media aritmética de la muestra es un estimador insesgado de la misma, ya que su esperanza (valor esperado) es igual a la media de la población.

En efecto, si una muestra X=(X₁,X₂,...,X_n)^t procede de una población de media μ, quiere decir que:

E [X i] = μ

para cualquier i=1...n

La media aritmética o media muestral,

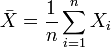$\bar X = \frac {1}{n} \sum_{i=1}^n X_i$ , con lo que, al aplicar las propiedades de linealidad de la esperanza matemática se tiene que:

$E[\bar X ] = E \left [ \frac {1}{n} \sum_{i=1}^n X_i \right ] =$

$= \frac {1}{n} E \left [ \sum_{i=1}^n X_i \right ] = \frac {1}{n}\sum_{i=1}^n E \left [ X_i \right ] =$

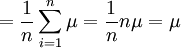
$= \frac {1}{n}\sum_{i=1}^n \mu= \frac {1}{n} n \mu = \mu$

Eficiencia

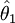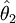Diremos que un estimador es más eficiente o más preciso que otro estimador, si la varianza del primero es menor que la del segundo. Por ejemplo, si $\hat \theta_1$ y $\hat \theta_2$ son ambos estimadores de $θ$ y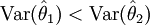

$\operatorname{Var}(\hat \theta_1) < \operatorname{Var}(\hat \theta_2)$

diremos que 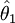$\hat \theta_1$ es más eficiente que 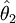$\hat \theta_2$ . Un estimador es más eficiente (más preciso), por tanto, cuanto menor es su varianza.

La eficiencia de los estimadores está limitada por las características de la distribución de probabilidad de la muestra de la que proceden. El teorema de Cramér-Rao determina que la varianza de un estimador insesgado 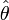$\hat \theta$ de un parámetro $θ$ es, como mínimo,

$\mathrm{var} \left(\widehat{\theta}\right) \geq \frac{1} { \mathrm{E} \left[ \left[ \frac{\partial}{\partial \theta} \log f(X;\theta) \right]^2 \right] }$

donde $f (X;θ)$ es la función de densidad de probabilidad de la muestra 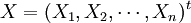$X=(X_1,X_2,\cdots,X_n)^t$ en función del parámetro $θ$ , (denominada función de verosimilitud). Si un estimador alcanza esta cota mínima, entonces se dice que el estimador es de mínima varianza.

Consistencia

Si no es posible emplear estimadores de mínima varianza, el requisito mínimo deseable para un estimador es que a medida que el tamaño de la muestra crece, el valor del estimador tienda a ser el valor del parámetro, propiedad que se denomina consistencia. Existen diversas definiciones de consistencia, más o menos restrictivas, pero la más utilizada es la denominada consistencia en media cuadrática que exige que:

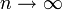
$E[\hat \theta] \to \theta$ cuando $n\to\infty$
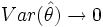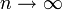
$Var(\hat \theta) \to 0$ cuando $n\to\infty$

Robustez

El estimador 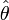$\hat \theta$ será un estimador robusto del parámetro $θ$ si la vulneración de los supuestos de partida en los que se basa la estimación (normalmente, atribuir a la población un determinado tipo de función de distribución que, en realidad, no es la correcta), no altera de manera significativa los resultados que éste proporciona.

Portal:Matemática Contenido relacionado con Matemática.

Suficiencia

Se dice que un estimador es suficiente cuando resume toda la información relevante contenida en la muestra, de forma que ningún otro estimador pueda proporcionar información adicional sobre el parámetro desconocido de la población.

Invarianza

Se dice que un estimador es invariante cuando el estimador de la función del parámetro coincide con la función del estimador del parámetro, $\left[ f(\theta) \right]^* = f(\theta^*)$ .

Ejemplo.- Si para estimar la varianza muestral utilizamos la varianza poblacional, entonces para estimar la desviación típica muestral será razonable utilizar la desviación típica poblacional.

Obtenido de "Estimador"

Categoría: Inferencia estadística

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

estimador — |ô| adj. s. m. Que ou aquele que estima; aquele que sabe estimar ou avaliar. ‣ Etimologia: estimar + dor … Dicionário da Língua Portuguesa
estimador — estimador, ra (Del lat. aestimātor, ōris). adj. Que estima. U. t. c. s. m.) … Diccionario de la lengua española
estimador — ► adjetivo Que estima. * * * estimador, a adj. y n. Que estima. * * * estimador, ra. (Del lat. aestimātor, ōris). adj. Que estima. U. t. c. s. m … Enciclopedia Universal
estimador — es|ti|ma|dor Mot Agut Nom masculí … Diccionari Català-Català
Estimación estadística — Saltar a navegación, búsqueda En inferencia estadística se llama estimación al conjunto de técnicas que permiten dar un valor aproximado de un parámetro de una población a partir de los datos proporcionados por una muestra. Por ejemplo, una… … Wikipedia Español
Máxima verosimilitud — En estadística, la estimación por máxima verosimilitud (conocida también como EMV y, en ocasiones, MLE por sus siglas en inglés) es un método habitual para ajustar un modelo y encontrar sus parámetros. Contenido 1 Historia 2 Fundamento 3… … Wikipedia Español
Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad … Wikipedia Español
Media truncada — Se denomina media truncada a una medida de tendencia central estadística, similar a un promedio y una mediana. Para el cálculo del promedio en este caso previamente se descartan porciones de la distribución de probabilidad o muestra en el extremo … Wikipedia Español
Teorema de Rao-Blackwell — En estadística el teorema de Rao Blackwell permite resolver la transformación de un estimador crudo arbitrario en uno optimizado mediante el criterio del error cuadrático medio u otro similar. El teorema de Rao Blackwell establece que si g(X) es… … Wikipedia Español
Cota de Cramér-Rao — Saltar a navegación, búsqueda En estadística, la cota de Cramér Rao (abreviada CRB por sus siglas del inglés) o cota inferior de Cramér Rao (CRLB), llamada así en honor a Harald Cramér y Calyampudi Radhakrishna Rao, expresa una cota inferior para … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Estimador

Estimador

Contenido