- Cúpula geodésica
-
Cúpula geodésica
Semiesfera geodésica de frecuencia 4 generada de un icosaedro.
Una cúpula geodésica es parte de una esfera geodésica, un poliedro generado a partir de un icosaedro o un dodecaedro, aunque puede generarse de cualquiera de los sólidos platónicos.
Descripción geométrica
Las caras de una cúpula geodésica pueden ser triángulos , Hexágonos o cualquier otro polígono. Los vértices deben coincidir todos con la superficie de una esfera o un elipsoide (si nos vértices no quedan en la superficie, la cúpula ya no es geodésica). El número de veces que las aristas del icosaedro o dodecaedro son subdivididas dando lugar a triángulos más pequeños se llama la frecuencia de la esfera o cúpula geodésica. Para la esfera geodésica se cumple el teorema de poliedros de Euler, que indica que:
C + V − A = 2
Donde C es el número de caras (o número de triángulos), V el número de vértices (o uniones múltiples) y A el número de aristas (o barras usadas). Para una cúpula parcial que no sea una esfera completa se cumple:
C + V − A = 1
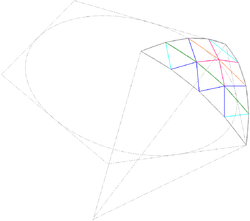Descripción de la subdivisión de una cara de un Dodecaedro con frecuencia 4.Para construir esferas geodésicas se utilizan las fórmulas de los radios del dodecaedro o icosaedro. Los radios permiten levantar los nuevos vértices de los subdivisiones a la superficie de la esfera que pasará por los vértices originales del cuerpo.
Estabilidad elástica
Las cúpulas geodésicas a diferencia de las cúpulas conformadas por celosías tridimensionales, pueden sufrir pandeo global sin que ninguno de los elementos que lo conforma haya sufrido pandeo. Es por eso que para grandes luces se requiere un cálculo no lineal para determinar sus cargas críticas y asegurarse de que no se producen fenómenos de inestabilidad elástica.
Enlaces externos
Categoría: Cúpulas
Wikimedia foundation. 2010.
