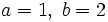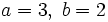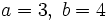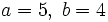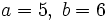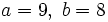- Curva de Lissajous
-
Curva de Lissajous
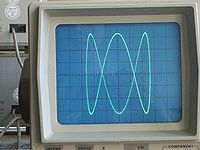 Curva de Lissajous en un osciloscopio.
Curva de Lissajous en un osciloscopio.
En matemáticas, la curva de Lissajous, también conocida como figura de Lissajous o curva de Bowditch, es la gráfica del sistema de ecuaciones paramétricas correspondiente a la superposición de dos movimientos armónicos simples en direcciones perpendiculares:
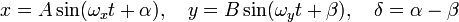
Esta familia de curvas fue investigada por Nathaniel Bowditch en 1815 y después, con mayores detalles, por Jules Antoine Lissajous.
Contenido
Propiedades
La apariencia de la figura es muy sensible a la relación
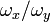 , esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si
, esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si 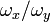 es un número racional, esto es, si
es un número racional, esto es, si 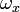 y
y 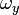 son conmensurables. Entonces existirán dos números naturales, nx y ny, tales que
son conmensurables. Entonces existirán dos números naturales, nx y ny, tales que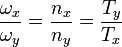
y, obviamente, el periodo del movimiento resultante es el valor de T
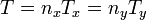
obtenido utilizando los valores más pequeños que satisfagan la relación (fracción irreducible).
La apariencia de estas curvas a menudo sugiere un nudo de tres dimensiones u otros tipos de nudos, incluyendo los conocidos como nudos de Lissajous, proyección en el plano de las figuras de Lissajous.
Uso en logotipos
Las figuras de Lissajous son usadas como logotipos. Ejemplos de estos logotipos son el de Australian Broadcasting Corporation (a = 1, b = 3, δ = π/2) y el del Lincoln Laboratory at MIT (a = 8, b = 6, δ = 0). Las curvas de Lissajous pueden ser trazadas mecánicamente por medio de un armonógrafo.
Espirógrafo
Es bastante parecido en aspecto a las curvas de Lissajous, pero con pequeñas diferencias en cuanto a las Matemáticas subyacentes.
Véase también
Referencias
Bibliografía
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons.
Enlaces externos
- Curva de Lissajous en Mathworld
- Figuras de Lissajous animadas en Java
- Sobre el logo de Australian Broadcasting Corporation
- Sobre el logo de MIT Lincoln Laboratory
- Herramienta libre QLiss3D mostrando figuras de Lissajous en 3D
- Lissajous: Visualización interactiva mostrando la identidad circular
Categorías: Física | Mecánica | Oscilaciones | Curvas
Wikimedia foundation. 2010.