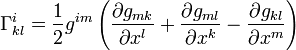Escalar de curvatura de Ricci
- Escalar de curvatura de Ricci
-
Escalar de curvatura de Ricci
En matemáticas, la curvatura escalar de una superficie es la familiar curvatura gaussiana. Para las variedades riemannianas de dimensión más alta (n > 2), es el doble de la suma de todas las curvaturas seccionales a lo largo de todos los 2-planos atravesados por un cierto marco ortonormal. Matemáticamente, la curvatura escalar, que suele designarse con las letras R o S, coincide también la traza total de la curvatura de Ricci así como del tensor de curvatura.
Expresión en componentes
La curvatura escalar de Ricci R puede expresarse fácilmente en términos del tensor métrico gμν(y sus derivadas primeras) que define la geometría de la superficie o variedad riemanniana cuya curvatura escalar pretendemos encontrar, usando el convenio de sumación de Einstein:
![R = -g^{\mu\nu}\left[\Gamma_{\mu\nu}^\lambda \Gamma_{\lambda\sigma}^\sigma -
\Gamma_{\mu\sigma}^\lambda \Gamma_{\nu\lambda}^\sigma \right]-\part_\nu\left[g^{\mu\nu} \Gamma^\sigma_{\mu\sigma} -g^{\mu\sigma} \Gamma^\nu_{\mu\sigma} \right]](/pictures/eswiki/51/314d8901136bef6202986dc54256c544.png)
Donde los símbolos de Christoffel que aparecen en la expresión anterior se calculan a partir de las derivadas primeras de las componentes del tensor métrico:
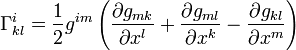
Categoría: Geometría diferencial
Wikimedia foundation.
2010.
Mira otros diccionarios:
Escalar de curvatura de Ricci — En matemáticas, la curvatura escalar de una superficie es la familiar curvatura gaussiana. Para las variedades de dimensión más alta, es el doble de la suma de todo las curvaturas seccionales a lo largo de todos los 2 planos atravesados por un… … Enciclopedia Universal
Tensor de curvatura — En geometría diferencial, el tensor de curvatura de Riemann , o simplemente tensor de curvatura o tensor de Riemann, supone una generalización del concepto de curvatura de Gauss, definido para superficies, a variedades de dimensiones arbitrarias … Wikipedia Español
Tensor de Ricci — En geometría diferencial, el tensor de curvatura de Ricci o simplemente, tensor de Ricci, que suele notarse por los símbolos Rab o Ric, es un tensor simétrico bivalente obtenido como una traza del tensor de curvatura, que, como aquel, puede… … Wikipedia Español
Tensor de Ricci — En geometría diferencial, la curvatura de Ricci es un tensor bivalente, obtenido como una traza del pleno tensor de curvatura. Puede ser pensado como un Laplaciano del tensor métrico riemaniano en el caso de las variedades de Riemann. En la… … Enciclopedia Universal
Introducción matemática a la relatividad general — La teoría de la relatividad general es una teoría métrica de la gravitación que incorpora además una descripción básica de los sistemas de referencia totalmente generales. Matemáticamente la teoría de la relatividad describe los efectos del campo … Wikipedia Español
Ecuación del campo de Einstein — Saltar a navegación, búsqueda En física, la ecuación del campo de Einstein o la ecuación de Einstein es una ecuación en la teoría de la gravitación, llamada relatividad general, que describe cómo la materia crea gravedad e, inversamente, cómo la… … Wikipedia Español
Campo gravitatorio — Saltar a navegación, búsqueda En física, el campo gravitatorio o campo gravitacional es un campo de fuerzas que representa la interacción gravitatoria. Si se dispone en cierta región del espacio una masa M, el espacio alrededor de M adquiere… … Wikipedia Español
Relatividad general — Algunas partes de este artículo pueden resultar complicadas, en ese caso se recomienda Introducción a la relatividad general Representación artística de la explosión de la supernova SN 2006gy, situada a 238 millones de años luz. De ser válido el… … Wikipedia Español
Símbolos de Christoffel — En matemáticas y física, los símbolos de Christoffel, así nombrados por Elwin Bruno Christoffel (1829 1900), son expresiones en coordenadas espaciales para la conexión de Levi Civita derivada del tensor métrico. Se utilizan los símbolos de… … Wikipedia Español
Teoría relativista de la gravitación — La teoría relativista de la gravitación (TRG) es una teoría del campo gravitatorio formulada, por Logunov, Mestvirishvili y Petrov. Dicha teoría construye una teoría del campo gravitatorio dentro de los límites de la teoría especial de la… … Wikipedia Español
