En física, la ecuación del campo de Einstein o la ecuación de Einstein es una ecuación en la teoría de la gravitación, llamada relatividad general, que describe cómo la materia crea gravedad e, inversamente, cómo la gravedad afecta la materia. La ecuación del campo de Einstein se reduce a la ley de Newton de la gravedad en el límite no-relativista, esto es, a velocidades bajas y campos gravitacionales débiles.

En la ecuación, la gravedad se da en términos de un tensor métrico, una cantidad que describe las propiedades geométricas del espacio-tiempo tetradimensional. La materia es descrita por su tensor de tensión-energía, una cantidad que contiene la densidad y la presión de la materia. Estos tensores son tensores simétricos 4 x 4, de modo que tienen 10 componentes independientes. Dada la libertad de elección de las cuatro coordenadas del espacio-tiempo, las ecuaciones independientes se reducen a 6. La fuerza de acoplamiento entre la materia y la gravedad es determinada por la constante gravitatoria universal.

Contenido 1 Forma matemática de la ecuación del campo de Einstein 2 Interpretación geométrica de la Ecuación de Einstein 3 Soluciones de la ecuación del campo de Einstein 3.1 Distribución de masa esférica simétrica y estática 3.2 Masa de simetría axial en rotación 3.3 Universo isótropo y homogéneo

Forma matemática de la ecuación del campo de Einstein

La ecuación del campo de Einstein describe cómo el espacio-tiempo se curva por la materia y, recíprocamente, cómo la materia es influida por la curvatura del espacio-tiempo, es decir, cómo la curvatura da lugar a gravedad.

La ecuación del campo se presenta como sigue:

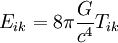
donde:

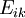es el tensor es la curvatura de Einstein, una ecuación diferencial de segundo orden en términos del tensor métrico 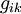, y 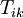es el tensor de tensión-energía. La constante de acoplamiento se da en términos de 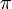, pi, , la velocidad de la luz y 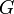, la constante gravitacional.

El tensor de la curvatura de Einstein se puede escribir como

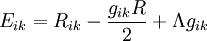
donde además 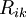es el tensor de curvatura de Ricci, 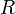es el escalar de curvatura de Ricci y 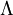es la constante cosmológica.

La ecuación del campo por lo tanto también puede darse como sigue:

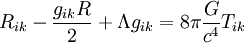
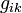es un tensor simétrico 4 x 4, así que tiene 10 componentes independientes. Dado la libertad de elección de las cuatro coordenadas del espacio-tiempo, las ecuaciones independientes se reducen en número a 6.

Estas ecuaciones son la base de la formulación matemática de la relatividad general.

Interpretación geométrica de la Ecuación de Einstein

La Teoría de la relatividad puso de manifiesto que la masa de los cuerpos depende del observador, pues ésta varía con su velocidad aparente, al igual que el concepto de simultaneidad, y por tanto también el espacio que se observa (formado por todos los sucesos simultáneos). Pues bien, la ecuación de Einstein puede enunciarse también afirmando que para cada observador, la curvatura escalar 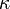del espacio es proporcional a la densidad aparente  :

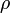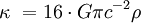
donde c = 3 × 10¹⁰ [cm s^-1] es la velocidad de la luz y G = 6,67 × 10^-8 [cm³ s^-2 g^-1] es la constante de la gravitación universal. De acuerdo con el significado geométrico de la curvatura escalar, esta igualdad afirma que en una esfera de masa M y densidad constante, el exceso radial (la diferencia entre el radio real y el radio que le correspondería en la geometría euclídea a una esfera de igual área) es igual a

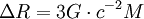
Por ejemplo, en el caso de la Tierra el exceso radial es de 0,15cm y en el caso del Sol es de unos 500 metros.

Es asombroso que esta ecuación, que introduce mínimas correcciones en las fórmulas de la geometría euclídea, recoja casi todas las ecuaciones conocidas de la Física macroscópica. En efecto, cuando la velocidad de la luz c tiende a infinito, de ella se derivan la Ley newtoniana de la Gravitación, la Ecuación de Poisson y, por tanto, el carácter atractivo de las fuerzas gravitatorias, las ecuaciones de la mecánica de fluidos (ecuación de continuidad y ecuaciones de Euler), las leyes de conservación de la masa y el momento, el carácter euclídeo del espacio, etc.

Igualmente se derivan todas la leyes de conservación relativistas, y que la existencia de campos gravitatorios y de masa sólo es posible cuando el espacio tiene dimensión mayor que 2. Más aún, si se supone que el espacio tiene dimensión 4 (las tres que vemos diariamente más una pequeñísima dimensión circular extra, aproximadamente del tamaño de la llamada longitud de Planck 10 ^{− 33}cm) de la ecuación de Einstein se deducen la teoría clásica del electromagnetismo: las Ecuaciones de Maxwell y, por tanto, la Ley de Coulomb, la Conservación de la carga eléctrica y la ley de Lorentz.

Soluciones de la ecuación del campo de Einstein

Una solución de la ecuación del campo de Einstein es cierta métrica apropiada para la distribución dada de la masa y de la presión de la materia. Algunas soluciones para una situación física dada son como sigue.

Distribución de masa esférica simétrica y estática

La solución para el vacío alrededor de una distribución de masa esférica simétrica, estática, es la métrica de Schwarzschild y la métrica de Kruskal-Szekeres. Se aplica a una estrella y conduce a la predicción de un horizonte de sucesos más allá del cual no se puede observar. Predice la posible existencia de un agujero negro de masa dada M del que no puede ser extraída ninguna energía, en el sentido clásico del término (i.e. no mecánico-cuántico).

Masa de simetría axial en rotación

La solución para el espacio vacío alrededor de una distribución de masa de simetría axial en rotación es la métrica de Kerr. Se aplica a una estrella que rota y conduce a la predicción de la existencia posible de un agujero negro en rotación de masa dada M y momento angular J, del cual la energía rotatoria puede ser extraída.

Universo isótropo y homogéneo

La solución para un Universo isótropo y homogéneo, lleno con una densidad constante y de una presión insignificante, es la métrica de Robertson-Walker. Se aplica al Universo en su totalidad y conduce a diversos modelos de su evolución que predicen un Universo en expansión.