Un deltaedro es un poliedro cuyas caras son triángulos equiláteros iguales. El nombre tiene su origen en el de la letra griega delta (Δ), cuya grafía mayúscula recuerda un triángulo equilátero.

Deltaedros convexos

Aunque existen infinitos deltaedros posibles, sólo ocho de ellos son convexos, y se listan a continuación:

Deltaedros convexos
Nombre		Imagen	Caras		Aristas	Vértices		Simetría
P1	Tetraedro regular		4	4 × te	6	4	4 × 3·3·3	Td
J12	Bipirámide triangular		6	6 × te	9	5	2 × 3·3·3 3 × 3·3·3·3	D3h
P3	Octaedro regular	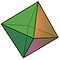	8	8 × te	12	6	6 × 3·3·3·3	Oh
J13	Bipirámide pentagonal	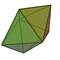	10	10 × te	15	7	5 × 3·3·3·3 2 × 3·3·3·3·3	D5h
J84	Biesfenoide romo		12	12 × te	18	8	4 × 3·3·3·3 4 × 3·3·3·3·3	D2d
J51	Prisma triangular triaumentado		14	14 × te	21	9	3 × 3·3·3·3 6 × 3·3·3·3·3	D3h
J17	Bipirámide cuadrada giroelongada		16	16 × te	24	10	2 × 3·3·3·3 8 × 3·3·3·3·3	D4d
P5	Icosaedro regular	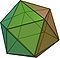	20	20 × te	30	12	12 × 3·3·3·3·3	Ih
te = Triángulos equiláteros

Sólo tres de los anteriores deltaedros son regulares (sólidos platónicos):

• El deltaedro de cuatro caras (tetraedro).
• El deltaedro de ocho caras (octaedro).
• El deltaedro de veinte caras (icosaedro).

Los otros cinco, aunque tengan sus caras regulares y uniformes, sus vértices no son uniformes. Por ello no son poliedros regulares, sino irregulares dentro de la particular familia de los sólidos de Jonhson, que son los sólidos convexos formados con caras polígonos regulares que no pertenecen a ninguna de las otras familias.

Los deltaedros retienen su forma, incluso aunque se permita a sus aristas girar libremente alrededor de los vértices. Esto no ocurre con todos los poliedros; por ejemplo, si se intenta lo mismo con un cubo, se comprobará que es posible colapsalo "doblándolo" para formar un prisma de base romboidal.

Deltaedros cóncavos

De entre los infinitos deltaedros cóncavos posibles, se listan los más notables:

• El Gran icosaedro, uno de los cuatro sólidos de Kepler-Poinsot.
• La Estrella octángula, la macla formada por dos tetraedros y estudiada por Kepler.
• La tercera estelación del icosaedro.