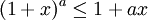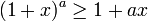- Desigualdad de Bernoulli
-
Desigualdad de Bernoulli
La inecuación de Bernoulli, es interesante por sí misma y es utilizada en la resolución de problemas.
Si
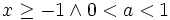 entonces
entoncesEn cambio si
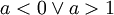 entonces
entoncesSi
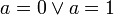 , la desigualdad se convierte en igualdad.Categorías: Álgebra | Desigualdades
, la desigualdad se convierte en igualdad.Categorías: Álgebra | Desigualdades
Wikimedia foundation. 2010.