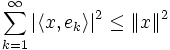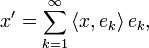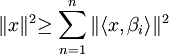Desigualdad de Bessel

Desigualdad de Bessel

Desigualdad de Bessel

En matemáticas, especialmente en análisis funcional, la desigualdad de bessel es una proposición acerca de los coeficientes de un elemento x en un espacio de Hilbert con respecto a una secuencia ortonormal.

Sea H un espacio de hilbert, suponga que e1,e2,... es una secuencia ortonormal en H. Entonces, paratodo x en H se tiene que

\sum_{k=1}^{\infty}\left\vert\left\langle x,e_k\right\rangle \right\vert^2 \le \left\Vert x\right\Vert^2

donde <·,·> denota el producto interior en el espacio de hilbert H, Si nosotros definimos la suma infinita

x' = \sum_{k=1}^{\infty}\left\langle x,e_k\right\rangle e_k,

La desigualdad de bessel nos dice que esta serie matemática converge.

Para una secuencia ortonormal completa (esto es, para una secuencia ortonormal que a la vez en una base ortonormal de H), nosotros tenemos la identidad de Parseval, que remplaza la desigualdad por una igualdad (y consecuentemente x' con x).

En Álgebra lineal la Desigualdad de Bessel estipula que dado un espacio vectorial V con producto interior definido, dada β = {β1,β2,...,βn} una subconjunto ortonormal de V. Se cumple que para todo x en V:

\lVert x \lVert ^{2}\geq\sum_{n=1}^{n} \|\langle x,\beta_{i}\rangle \|^{2}
Obtenido de "Desigualdad de Bessel"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Desigualdad de Cauchy-Schwarz — Saltar a navegación, búsqueda En matemáticas, la desigualdad de Cauchy Schwarz, también conocida como desigualdad de Schwarz, desigualdad de Cauchy, o la desigualdad de Cauchy Bunyakovski Schwarz es una desigualdad muy útil encontrada en… …   Wikipedia Español

  • Identidad de Parseval — En análisis matemático, la identidad de Parseval, también conocida como la igualdad de Parseval, es una generalización del teorema de Pitágoras aplicado a los espacios de Hilbert separables. Si B es una base ortonormal en un espacio vectorial,… …   Wikipedia Español

  • Relación de Parseval — En matemáticas, la Relación de Parseval demuestra que la Transformada de Fourier es unitaria; es decir, que la suma (o la integral) del cuadrado de una función es igual a la suma (o a la integral) del cuadrado de su transformada. Esta relación… …   Wikipedia Español

  • Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”