Espacios Lp

Espacios Lp: Espacios Lp

Saltar a navegación, búsqueda

Los espacios $L p$ son los espacios vectoriales normados más importantes en el contexto de la teoría de la medida y de la integral de Lebesgue. Reciben también el nombre de espacio de Lebesgue por el matematico Henri Lebesgue.

Contenido

1 Definición

2 Propiedades

3 Algunos Ejemplos Importantes

4 Véase también

Definición

Consideremos $(X, Σ, μ)$ un espacio de medida. Se define el espacio vectorial:

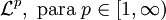
$\mathcal{L}^p,\ \mbox{para}\ p \in [1, \infty)$

Como el espacio de todas las funciones medibles 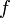$f\,$ que cumplen: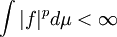

$\int |f|^p d\mu < \infty$

Asimismo, se define el espacio 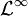$\mathcal{L}^\infty\,$ como el espacio de las funciones medibles 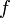$f\,$ que verifican: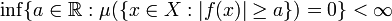

$\inf \{a \in \mathbb{R}: \mu(\{x \in X: |f(x)|\geq a\})=0\} <\infty$

Es decir, aquellas funciones medibles acotadas ctp. Una norma natural para definir en estos espacios sería:

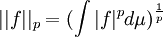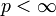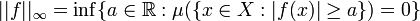
$||f||_p=(\int |f|^p d\mu)^{\frac1p}$ , si $p<\infty$ , y $||f||_\infty=\inf \{a \in \mathbb{R}: \mu(\{x \in X: |f(x)|\geq a\})=0\}$

Sin embargo, una aplicación así definida no resulta norma, ya que no se cumple 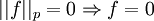$||f||_p=0 \Rightarrow f=0$ , pues cualquier función que sea igual a la función nula, salvo en un conjunto de medida nula, tendrá norma cero.

Así, se define la siguiente relación de equivalencia $R$ sobre 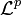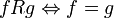$\mathcal{L}^p$ : $fRg \Leftrightarrow f=g$ $c t p$ . Se prueba que efectivamente es una relación de equivalencia, y se defina 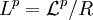$L^p=\mathcal{L}^p/R$ , i.e., el espacio vectorial cuyos elementos son las clases de equivalencia de la relación $R$ . Considerando entonces sobre $L p$ las normas anteriormente definidas (donde $f$ es cualquier representante de la clase de equivalencia), se prueba que 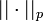$||\cdot||_p$ resulta ser norma y que su valor no depende del representante de la clase de equivalencia escogido. Usualmente no se hace distinción entre función y clase de equivalencia en este contexto.

Propiedades

$L p$ es Banach

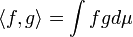$L 2$ es un Espacio de Hilbert, dotado del producto interno $\langle f,g\rangle=\int fg d\mu$ .

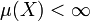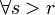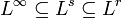Si $\mu(X)<\infty$ , entonces $\forall s><span class=$ r" style="max-width : 98%; height: auto; width: auto;" src="/pictures/eswiki/54/6df5a336abe70b551b2538529b6eb7a2.png"> se tiene que $L^\infty \subseteq L^s \subseteq L^r$ .

Si 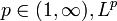$p \in (1, \infty), L^p$ es reflexivo

Si denotamos por $Ε$ al espacio de las funciones simples, se cumple que 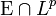$\Epsilon \cap L^p$ es denso en $L p$ .

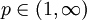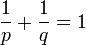Si $p \in (1, \infty)$ , el dual topológico de $L p$ es $L q$ donde $q$ es tal que $\frac1p + \frac1q=1$ .

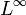Si el espacio de medida es $σ$ -finito, entonces el dual de $L 1$ se identifica con $L^\infty$ .

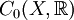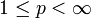Si $(X, Θ)$ es un espacio topológico localmente compacto separado, y $μ$ es una medida regular, entonces $C_0(X, \mathbb{R})$ (el espacio de las funciones continuas a soporte compacto) es denso en $L p$ con $1\leq p<\infty$ .

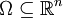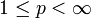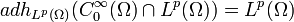El espacio de las funciones infinitamente derivables en un abierto $\Omega\subseteq\mathbb{R}^n$ a soporte compacto y que están en $L p$ con $1\leq p<\infty$ , es denso en $L p$ , es decir $adh_{L^p(\Omega)}(C_0^{\infty}(\Omega)\cap L^p(\Omega))=L^p(\Omega)$ .

Algunos Ejemplos Importantes

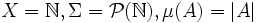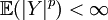Si $X=\mathbb{N}, \Sigma=\mathcal{P}(\mathbb{N}), \mu(A)=|A|$ (su cardinalidad), entonces $L p =$ variables aleatorias $Y$ que cumplen $\mathbb{E}(|Y|^p)<\infty$ .

Si 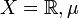$X=\mathbb{R}, \mu$ es la Medida de Lebesgue, entonces el espacio es el de las funciones a una variable real usuales, con la medida usual en $\mathbb{R}$ .

Véase también

Espacio de Sóbolev

Obtenido de "Espacios Lp"

Categorías: Teoría de la medida | Análisis funcional

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Espacios naturales de la Región de Murcia — Saltar a navegación, búsqueda Véase también: Medio ambiente de la Región de Murcia El relieve y el clima son los elementos principales que han configurado los espacios naturales en la Región de Murcia, originando importantes contrastes y una gran … Wikipedia Español
Espacios naturales de Cartagena (España) — Saltar a navegación, búsqueda El territorio de Cartagena, a pesar de la intensa explotación minera, turística e industrial que ha sufrido durante siglos, alberga una extraordinaria riqueza y diversidad natural, con un alto grado de endemismos… … Wikipedia Español
Espacios naturales de la provincia de Guadalajara — Saltar a navegación, búsqueda Espacios naturales protegidos La provincia de Guadalajara, dada su amplia y variada realidad geográfica, reune en su territorio, diversas condiciones climáticas, ya que se localiza en la zona de transición entre el… … Wikipedia Español
Espacios de nombres XML — Saltar a navegación, búsqueda Un espacio de nombres XML es una recomendación W3C para proporcionar elementos y atributos con nombre único en una instancia XML. Una instancia XML puede contener nombres de elementos o atributos procedentes de más… … Wikipedia Español
Espacios abiertos e islas del Mar Menor — Saltar a navegación, búsqueda Localización de estos espacios protegidos en verde oscuro en el Campo de Cartagena Mar Menor Espaci … Wikipedia Español
Espacios naturales de España — Saltar a navegación, búsqueda Artículo principal: Anexo:Espacios naturales de España La superficie que goza en España de algún tipo de protección sobrepasa los tres millones y medio de hectáreas y afecta a más de seiscientos espacios, alcanzando… … Wikipedia Español
Espacios Del Mundo — (Carenas,Испания) Категория отеля: Адрес: Arrabal, 19, 50212 Carenas, Испания … Каталог отелей
Espacios compartidos — Saltar a navegación, búsqueda El Espacio compartido, a veces llamado Superficie Compartida, es una teoría relativa a la organización del tráfico consistente en eliminar la separación tradicional entre automóviles, peatones y otros usuarios. El… … Wikipedia Español
Espacios Suites Posada — (Coatzacoalcos,Мексика) Категория отеля: Адрес: Avenida Benito Juarez Colon … Каталог отелей
Espacios Placeres Arte (revista) — Saltar a navegación, búsqueda Revista Espacios Placeres Arte, conocida también como revista EPA, fue una publicación independiente de divulgación artística cultural surgida en la provincia de Mendoza (Argentina) de alcance Nacional. El objetivo… … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos