Mapa de Karnaugh

Ejemplo de mapa de Karnaugh.

Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.

Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones redundantes.

El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2^N filas, el mapa K correspondiente debe poseer también 2^N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh se pueden utilizar para funciones de hasta 6 variables.

Ejemplo

Dada la siguiente función algebraica Booleana representada como el sumatorio de sus minitérminos, y con las variables Booleanas A, B, C, D, la función se puede representar con dos notaciones distintas:

• f(A,B,C,D) = ∑(6,8,9,10,11,12,13,14)
• 

Tabla de verdad

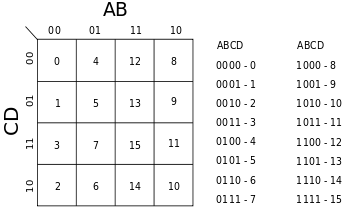
Utilizando los minitérminos definidos, se elabora la tabla de verdad:

Mapa de Karnaugh

Construcción del mapa-K.

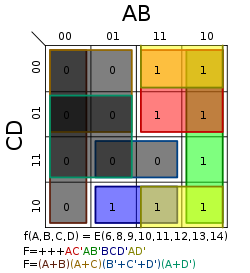
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadricula de 4 × 4.

La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 1 porque el resultado de la función es ƒ = 1 cuando A = 1, B = 0, C = 1, D = 0.

Una vez construido el mapa de Karnaugh, la siguiente tarea es la de seleccionar conjuntos de términos de manera que se obtenga el menor número de términos posible. Estos términos se seleccionan formando grupos de rectángulos cuyas areas sean potencia de 2 (ej. 1, 2, 4, 8, ...) tratando de agrupar el mayor número de términos posible.

Que términos seleccionar van dependiendo de como se quiera realizar la simplificación, puesto que esta puede realizarse por minitérminos o por maxitérminos.

Otro ejemplo

X1 X3 __________ 54645454 __________ 0 4 5 1 X4| 8 12 13 9 X2| | 10 14 15 11

 |                 2       6       7       3

Números correspondientes a las posiciones de la tabla de la verdad

Ejemplo mapa de Karnaugh:

                                        X1      
                                X3      _________       
                                _________               
                        0       1       1       1
        X4|             0       0       1       1
X2|       |             0       0       1       0
  |                     1       1       0       0

Tabla de lazos que se pueden permitir, según las variables que contenga un mapa: MAPAS según su variable

v      1        2       4       8       16      32      64
2       2       1       C       NA      NA      NA      NA
3       3       2       1       C       NA      NA      NA
4       4       3       2       1       C       NA      NA
5       5       4       3       2       1       C       NA
6       6       5       4       3       2       1       C

v= variables
C= constantes
NA= no permitido

Software

Software disponible para asistir el mapeo de Karnaugh:

• GKMap
• Karnaugh Map Minimizer
• WinLogiLab
• Boolean Calculator: VK, Truth Tables,...
• Karma, un conjunto de herramientas de síntesis lógica, incluyendo mapas de Karnaugh, la minimización de Quine-McCluskey, la enseñanza del módulo y más. Logic Circuit

Synthesis Labs (LogiCS) - UFRGS, Brazil.

• Gorgeous Karnaugh K-Maps minimization software