Tabla de Young

En matemáticas, una tabla de Young es un objeto combinatorio relacionado con teoría de representaciones y funciones simétricas. Deben su nombre al matemático inglés Alfred Young, quien las estudió en 1900 y que fueron luego usadas por Georg Frobenius para estudiar el grupo simétrico.

Las tablas de Young están estrechamente relacionadas con representaciones de grupos, especialmente grupos lineales y simétricos. Son objetos de estudio en el área de combinatoria algebraica.

Diagrama de Young

Diagrama de Young de forma (4,2,1,1)

Para poder definir una tabla de Young, es preciso definir primero un diagrama de Young, también llamado diagrama de Ferrers, el cual es un arreglo de casillas dispuestas por filas de modo que cada fila tiene una cantidad menor o igual de casillas que la fila anterior. De esta forma, listar el número de casillas en cada fila proporciona una sucesión (débilmente) decreciente de enteros positivos, es decir una partición λ de n, el número total de casillas.

Dado un diagrama de Young D, la partición obtenida listando el número de casillas de cada fila se conoce como forma del diagrama. De manera inversa, dada una partición λ es posible construir el diagrama correspondiente a λ, por lo que suele establecerse una identificación entre los diagramas y sus formas.

Diagrama de Young de forma (4,2,1,1), representación francesa. Se destaca la casilla (2,3).

Cuando se listan las columnas de un diagrama de Young también se obtiene una partición μ llamada partición conjugada de λ, lo cual se simboliza como μ=λ'. El diagrama de forma λ' se obtiene reflejando el diagrama de forma λ sobre la diagonal principal.

La forma descrita de representar las particiones (iniciando en la parte superior y decreciendo hacia abajo) se conoce como la forma inglesa, y en ésta, las casillas se indican de forma similar a una matriz. Sin embargo, en los países de habla francesa suelen representarse con la mayor fila en la parte inferior, decreciendo hacia arriba. Con esta convención, las casillas se nombran de forma similar a coordenadas cartesianas (aunque listando primero el eje vertical), recibiendo esta convención el nombre de forma francesa.

Cuando en lugar de casillas se usan puntos, el diagrama se conoce como Diagrama de Ferrers

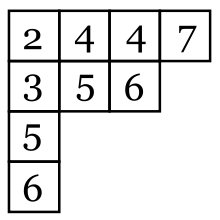
Tabla de Young

Tabla de Young semiestándar de forma (4,2,1,1) y contenido (0,1,1,2,2,2,1)

Tabla de Young estándar de forma (4,2,1,1)

Si d_k es el número de veces Una llenado de una tabla de Young se obtiene colocando un entero positivo en cada casilla de de un diagrama de Young.

que aparece el entero k al llenar la tabla, el contenido de la tabla es el vector (d₁, d₂, ..., d_j,...), el cual no necesariamente es una partición.

Una tabla de Young, es un llenado en el que las filas son débilmente crecientes mientras que las columnas son estrictamente decrecientes. Una tabla que satisface esas condiciones se denomina también tabla de Young semiestándar, cuando se quiere diferenciar de otras formas de llenado más específicas.

Cuando una tabla de Young con n casillas es llenada con los números 1,2,3,...,n (sin repetir), recibe el nombre de tabla de Young estándar. De forma equivalente, una tabla de Young estándar es una tabla semiestándar cuyo contenido es (1, 1, ..., 1).

Las definiciones anteriores también tienen sentido si se usan elementos de un conjunto totalmente ordenado (para poder comparar «mayor» y «menor»), aunque rara vez se consideran diagramas cuyas casillas no se rellenan con enteros positivos.

A diferencia de los diagramas, en los que transponer (reflejar respecto a la diagonal) da origen a un nuevo diagrama, en las tablas esto usualmente no es posible. Sin embargo, en el caso especial de tablas de Young estándar, el resultado de reflejar respecto a la diagonal es nuevamente una tabla de Young estándar cuya forma es conjugada respecto a la forma de la original.

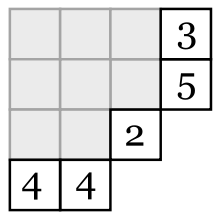
Tabla de Young sesgada

Tabla de Young sesgada de forma (4,4,3,2)/(3,3,2)

Un diagrama de Young sesgado consiste en un diagrama de Young al que se le borra un diagrama de Young más pequeño. Si el diagrama de Young mayor tiene forma λ y el menor tiene forma μ, entonces la forma del diagrama sesgado se denota por λ/μ.

Una tabla de Young sesgada es entonces el llenado de un diagrama sesgado de forma que las filas sean débilmente decrecientes y las columnas estrictamente crecientes.

Las tablas de Young sesgadas son generalizaciones de las tablas de Young, dado que estas últimas se obtienen cuando μ es un diagrama vacío.

Referencias

Fulton, William (1997). Young Tableaux: With Applications to Representation Theory and Geometry (1a ed. edición). Cambridge University Press. pp. 260 pp.. ISBN 0-521-56144-2.