Grupo lineal

Grupo lineal

Grupo lineal


El grupo lineal de un espacio vectorial E, denotdo como GL(E), es el grupo formado por todas los isomorfismos de ese espacio.

Grupo lineal del espacio euclídeo

Si consideramos el espacio euclídeo n-dimensional o 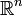\R^n como espacio vectorial su grupo lineal estará representado por todas las aplicaciones lineales que admiten inversa. Si escojemos una base cualquiera para ese espacio vectorial, cada aplicación lineal podría expresarse mediante una matriz. Entonces el grupo lineal vendrá representado por el conjunto de todas las matrices que represetan aplicaciones lineales que admiten inversa, y por tanto, por matrices cuyo determinante es diferente de cero (ya que el álgebra lineal establece que una aplicación lineal invertible viene representada en una base por una matriz de determinante diferente de cero).

Propiedades del grupo lineal

En un espacio vectorial normado E el grupo lineal GL(E) puede ser dotado de una topología inducida, y resulta ser un conjunto abierto dentro del conjunto de aplicaciones lineales o morfismos del espacio vectorial E.

Obtenido de "Grupo lineal"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Grupo lineal general — En matemáticas, el grupo lineal general (GL) de un espacio vectorial , denotdo como , es el grupo formado por todos los isomorfismos de ese espacio. Cuando el espacio vectorial es siendo un cuerpo F (tal como o …   Wikipedia Español

  • Grupo — (del italiano gruppo), la pluralidad de elementos que forman un conjunto, puede hacer referencia a: Contenido 1 En matemáticas 2 En astronomía 3 En física …   Wikipedia Español

  • Grupo de Lorentz — En física, el grupo de Lorentz es el grupo de todas las transformaciones de Lorentz del espacio de Minkowski, la composición clásica de todas los fenómenos físicos no gravitacionales. Es el grupo de isometría grande posible que deja invariante el …   Wikipedia Español

  • Grupo (matemática) — En álgebra abstracta, un grupo es un conjunto en el que se define una operación binaria (i.e. un magma), que satisface ciertos axiomas detallados más abajo. La rama de la matemática que estudia los grupos se llama teoría de grupos. Contenido 1… …   Wikipedia Español

  • Grupo ortogonal — En matemáticas, el grupo ortogonal de grado n sobre un cuerpo F (escrito como O(n, F)) es el grupo de matrices ortogonales n por n con las entrad …   Enciclopedia Universal

  • Grupo alquilo — Grupo metilo CH3, unido a una cadena de cinco átomos de carbono (pentano), formando el 3 metilpentano. El grupo alquilo (nombre derivado de alcano con la terminación ilo) es un grupo funcional orgánico monovalente, formado por la separación de un …   Wikipedia Español

  • Lineal B — Tipo Silabario con ideogramas adicionales Idiomas Griego micénico Época HR IIA HR III B2 1450 a. C. 1200 a. C …   Wikipedia Español

  • Grupo de Lie — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Lineal — Para otros usos de este término, véase Lineal (distribución comercial). La palabra lineal viene de la palabra latín linearis, que significa creado por líneas . Contenido 1 Matemáticas (función lineal) 1.1 Propiedades 1.2 …   Wikipedia Español

  • Lineal (distribución comercial) — Lineales en un supermercado. En el ámbito de las distribución comercial, se llama lineal al espacio donde se presentan o exponen los productos para su venta, en régimen de libre servicio. Este espacio puede ser el conjunto de estantes de las… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”