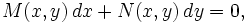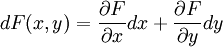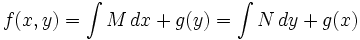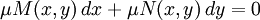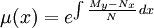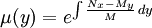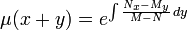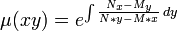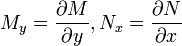- Ecuación diferencial exacta
-
Ecuación diferencial exacta
En matemáticas, una ecuación diferencial exacta es una ecuación diferencial ordinaria de primer orden que presenta la forma:
en donde las derivadas parciales de las funciones M y N:
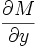 y
y 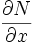 son iguales. Esto es equivalente a decir que existe una función F(x,y)=0 tal que
son iguales. Esto es equivalente a decir que existe una función F(x,y)=0 tal quedonde
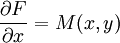 y
y 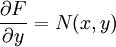 . Dado que F(x,y) es una función diferenciable entonces las derivadas cruzadas deben ser iguales y esta es la condición
. Dado que F(x,y) es una función diferenciable entonces las derivadas cruzadas deben ser iguales y esta es la condición 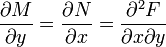 .
.Contenido
Método de resolución.
Para resolver una ecuación diferencial de este tipo, se ha de seguir los siguientes pasos:
- Comprobar la exactitud de la ecuación, esto es, verificar si las derivadas parciales de M (con respecto a y) y de N (con respecto a x) son iguales.
- Se integra M o N a conveniencia (M respecto a x o N respecto a y) obteniéndose de este modo la solución general de la ecuación aunque con una función incógnita g que aparece como constante de integración. Esto es:
- Para despejar la función g se deriva
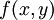 con respecto a la variable independiente de g.
con respecto a la variable independiente de g.
- Se iguala g' con M o N (si se integró M se iguala a N y viceversa.), despejando y luego integrando con respecto a la variable dependiente de g; de este modo se encontrará la función g.
- Finalmente se reemplaza el g encontrado en la solución general
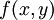 .
.
Factor integrante.
Si una ecuación diferencial no es exacta, pudiera llegar a serlo si se la multiplica por una función especial
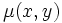 llamada factor integrante, tal que:
llamada factor integrante, tal que:Sea exacta.
Cabe destacar que bajo ciertas condiciones el factor integrante siempre existe, pero sólo para algunas formas de ecuaciones diferenciales es posible facilmente encontrar un factor integrante:
Factor integrante solo en función de x.
Si la ecuación diferencial posee un factor integrante respecto a x (es decir,
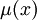 ), entonces se puede encontrar por medio de la fórmula siguiente:
), entonces se puede encontrar por medio de la fórmula siguiente:Factor integrante solo en función de y.
Si la ecuación diferencial posee un factor integrante respecto a y (es decir,
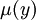 ), entonces se puede encontrar por medio de la fórmula siguiente:
), entonces se puede encontrar por medio de la fórmula siguiente:Factor integrante solo en función de x+y.
Si la ecuación diferencial posee un factor integrante respecto a x+y (es decir,
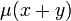 ), entonces se puede encontrar por medio de la fórmula siguiente:
), entonces se puede encontrar por medio de la fórmula siguiente:Factor integrante solo en función de x·y.
Si la ecuación diferencial posee un factor integrante respecto a x·y (es decir,
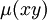 ), entonces se puede encontrar por medio de la fórmula siguiente:
), entonces se puede encontrar por medio de la fórmula siguiente:Donde M * x = M·x
Cabe mencionar que:
Bibliografía
- Tom M. Apostol (1979): Análisis matemático. ISBN 84-291-5004-8.
- Zill, Dennis G. (2006): Ecuaciones Diferenciales con Aplicaciones de Modelado. Octava edición. Thomson Learning Iberoamericana. México D.F., México. ISBN 970-686-487-3.
- Olivos, Elena; Mansilla, Angélica (2005): Ecuaciones Diferenciales, 100 Problemas Resueltos. Primera Edición. Editorial Universidad de La Frontera. Temuco, Chile.
Véase también.
- Ecuación diferencial
- Ecuación diferencial de primer orden
Categoría: Ecuaciones diferenciales ordinarias
Wikimedia foundation. 2010.