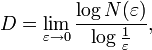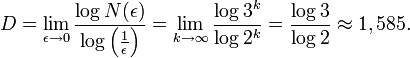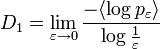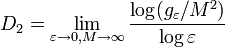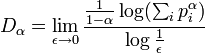- Dimensión fractal
-
Dimensión fractal
En geometría de fractales, la dimensión fractal, D es una cantidad estadística que da una idea de cuán completamente parece llenar un fractal el espacio conforme se amplía el primero hacia escalas más y más finas. Hay muchas definiciones específicas de dimensiones fractales y ninguna debería ser tratada como universal. Desde un punto de vista teórico, las más importantes de ellas son la dimensión de Hausdorff, la dimensión de empaquetamiento y, de forma más general, las dimensiones de Rényi. Por otro lado, la dimensión de conteo de cajas y la dimensión de correlación son ampliamente usadas en la práctica, en parte por su fácil implementación.
Aunque para algunos fractales clásicos todas estas dimensiones coinciden, en general no son equivalentes. Por ejemplo, la dimensión del copo de nieve de Koch tiene una dimensión topológica de uno, pero no puede ser tratada como una curva; la longitud entre cualesquiera dos puntos en el fractal es infinita. Ningún segmento del fractal tiene parecido a una línea, pero tampoco tiene parecido a una parte de un plano. En cierta forma se podría decir que es demasiado grande para poder ser considerada como un objeto unidimensional, pero es demasiado fina para ser considerada un objeto bidimensional. Esto lleva a la pregunta de si su dimensión se describe mejor con un número entre uno y dos. Ésta es una manera simple de motivar la idea de dimensión fractal.
Contenido
Definiciones
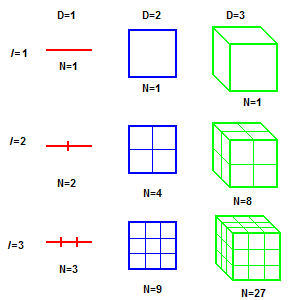
Fig.(1) Otra forma de definir la dimensión[1]
Hay principalmente dos formas aproximadas para generar una estructura fractal. Una es hacerla crecer a partir de un objeto y la otra es construir las divisiones subsecuentes de una estructura original como en el triángulo de Sierpinski (Fig.(2)).[2] En este caso se sigue la segunda aproximación para definir la dimensión de las estructuras fractales.
Si se toma un objeto con un tamaño lineal igual a 1 en una dimensión euclideana D, y se reduce su tamaño por un factor de 1 / l en cada dirección espacial, se necesitan un número N = lD de objetos autosimilares para cubrir el objeto original (Fig.(1)). Sin embargo, al despejar para D, la dimensión definida por
.
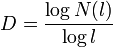es igual todavía a su dimensión topológica o euclideana.[1] Aplicando la ecuación anterior a una estructura fractal, se puede obtener la dimensión de la misma (que es más o menos la dimensión de Hausdorff) como un número no entero, como se esperaba.
donde
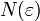es el número de estructuras autosimilares de lado lineal ε que se necesitan para cubrir toda la estructura.Por ejemplo, la dimensión fractal para el triángulo de Sierpinski (Fig.(2)) está dado por,
Fig.(2) Triángulo de SierpinskiOtras cantidades dimensionales incluyen la «dimensión de información» que considera cómo se escala la información promedio que se necesita para identificar una caja ocupada, conforme las cajas se vuelven más pequeñas:
y la dimensión de correlación, quizá la más fácil de calcular,
donde M es el número de puntos utilizados para generar una representación del fractal y gε es el número de pares de puntos que se encuentran más cercanos uno al otro que ε.
Dimensiones de Rényi
Las tres anteriores pueden verse como casos especiales de las dimensiones de Rényi de orden α, definidas como
El numerador es la llamada entropía de Rényi de orden α. La dimensión de Rényi con α=0 trata a todas las partes del atractor de manera similar, pero para valores más grandes de α se da un mayor peso en el cálculo a las partes del atractor que son visitadas con mayor frecuencia.
Un atractor para el cual las dimensiones de Rényi no son todas iguales es conocido como un multifractal, o se dice que muestra estructura multifractal. Esto es una señal de que un comportamiento a escala diferente ocurre en diferentes partes del atractor.
Estimación de la dimensión fractal para casos reales
Los cálculos de dimensiones fractales descritos arriba se obtienen a partir de fractales definidos formalmente. Sin embargo, ciertos fenómenos y objetos de la vida real pueden mostrar propiedades fractales, por lo que puede ser útil obtener la dimensión fractal de un conjunto de datos de una muestra. El cálculo de la dimensión fractal no se puede obtener de forma exacta sino que debe estimarse. Esto se usa en una variedad de áreas de investigación tales como la física,[3] análisis de imagen,[4] acústica,[5] ceros de la función zeta de Riemann[6] e incluso procesos electroquímicos.[7]
Las estimaciones prácticas de las dimensiones fractales son muy sensibles al ruido numérico o experimental, y particularmente a las limitaciones en la cantidad de datos. Cualquier afirmación basada en estimaciones de dimensiones fractales deben tomarse con cuidado puesto que hay un límite superior inevitable, a menos que se presenten cantidades muy grandes de datos.
Referencias
- Todo o parte de este artículo fue creado a partir de la traducción del artículo fractal dimension de la Wikipedia en inglés, bajo licencia Creative Commons Compartir Igual 3.0. y GFDL.
Notas
- ↑ a b Fractals & the Fractal Dimension
- ↑ Fluctuations and Scaling in Biology. Edited by T. Vicsek, 2001
- ↑ B. Dubuc, J. F. Quiniou, C. Roques-Carmes, C. Tricot, and S. W. Zucker, Plantilla:Doi-inline, Phys. Rev. A, 39 (1989), pp. 1500–1512.
- ↑ P. Soille and J.-F. Rivest, On the validity of fractal dimension measurements in image analysis, Journal of Visual Communication and Image Rep- resentation, 7 (1996), pp. 217–229.
- ↑ P. Maragos and A. Potamianos, Plantilla:Doi-inline, The Journal of the Acoustical Society of America, 105 (1999), p. 1925.
- ↑ O. Shanker (2006). «Random matrices, generalized zeta functions and self-similarity of zero distributions» J. Phys. A: Math. Gen.. Vol. 39. pp. 13983–13997. DOI 10.1088/0305-4470/39/45/008.
- ↑ Ali Eftekhari, Fractal Dimension of Electrochemical Reactions Journal of the Electrochemical Society, 2004, 151 (9), E291 – E296.
Bibliografía
- Mandelbrot, Benoît B., The (Mis)Behavior of Markets, A Fractal View of Risk, Ruin and Reward (Basic Books, 2004)
Categoría: Dimensión
Wikimedia foundation. 2010.
