Multifractal

Un multifractal un conjunto multifractal es una clase de conjunto fractal formado por una jerarquía de subconjuntos (variedades), cada uno de ellos de carácter fractal (variedades fractales). Por lo general, se considera que el multifractal es una variedad topológica, generalmente métrica. Un conjunto multifractal es un conjunto cuya dimensión de Hausdorff-Besicovitch excede a su dimensión topológica (D_HB > D_T, fractal "en el sentido de Mandelbrot"), pero cuyas dimensiones de Rényi superiores son diferentes de la dimensión de Hausdorff-Besicovitch. En un conjunto multifractal la dimensión de Hausdorff-Besicovitch difiere de la dimensión de información y de a la dimensión de correlación (que a su vez difieren entre sí).

Introducción

Un objeto multifractal es más complejo que un fractal simple autoescalante de dimensión fractal constante. Si un fractal de dimensión constante está complemente descrito por su dimensión fractal o "exponente fractal" (y en parte por su lagunaridad), la caracterización de un objeto multifractal requiere especificar un "espectro de exponentes" (llamado también "espectro de singularidad").

Cualquier reunión de conjuntos fractales por sí sola no puede considerarse un multifractal; para ello es necesario que estén coordinados de cierta manera. Como norma general, se exige que el espectro de singularidad sea una curva convexa. El objetivo es garantizar que el conjunto, y cada una de sus partes sea invariante bajo transformaciones de cambio de escala.

Los objetos aproxiadamente multifractales son comunes en la naturaleza y aparecen en geofísica, hidrodinámica (flujos turbulentos), astrofísica (evolución de las manchas solares) y cosmología (distribución de galaxias), así como en sistemas sociales como en series temporales del mercado de valores.

Ejemplos en la naturaleza

Flujos turbulentos

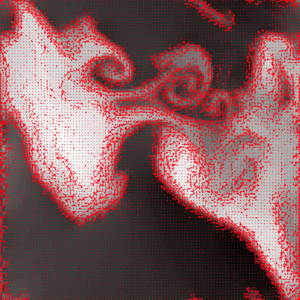
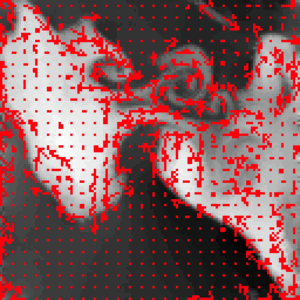
• El interés por los multifractales nace del estudio de las propiedades de los fluidos turbulentos con alto Número de Reynolds. Éstos son los llamados fluidos en régimen de Turbulencia Completamente Desarrollada. En esos caso, la elevada turbulencia del fluido hace que su estructura abandone todas las simetrías afines propias del régimen laminar. A cualquier escala a la cual se analice el fluido se encontrará que los grados de libertad no resueltos no son pequeñas variaciones o fluctuaciones sobre el régimen de mayor escala, sino que tienen amplitudes considerables, hasta el punto de que la dirección de la corriente está complemente indeterminada aunque se conozca, aunque se conozca la dirección a una escala mayor.

Campo de velocidades en flujo turbulento
(alta resolución)	(baja resolución)

Distribución de galaxias

Otro ejemplo de multifractal es la distribución de galaxias. Las estimaciones disponibles sugieren que el universo es más bien un objeto multifractal cuya dimensión de Hausdorff-Besicovitch sería D₀ ~ 2,1±0,1 y cuya dimensión de correlación D₂ ~ 1,3±0,1.^[1]

Descripción

Dado un sistema multifractal y una magnitud física medida sobre él tiene localmente un comportamiento cualitativo dado por una ley potencial de la forma:

El exponente se llama exponente de singularidad ya que describe localmente el grado de singularidad o regularidad que presenta el comportamiento de la magnitud dada alrededor del punto . Es obvio por ejemplo que si entonces la magnitud presentará discontinuidades, ya que la derivada no existe por culpa de que el límite que la define no es finito.

El conjunto formado por todos los puntos que comparten el mismo exponente de singularidad se llama "variedad de singularidad de exponente h". La variedad de singularidad de exponente h es un conjunto fractal de dimensión D(h). La curva definida como el grafo de la función D(h), es lo que se llama espectro de singularidad y describe completamente la distribución (estadística) de la magntiud .

En la práctica sin embargo, el comportamiento de un sistema multifractal no se caracteriza directamente por su espectro de singularidad, sino más bien mediante los "exponentes multiescala" . Frecuentemente los magnitudes medibles de sistemas multifractales siguen una ley de invariancia de escala asociada a leyes potenciales asociadas a la escala a. Dependiendo del objeto de estudio, dichas magnitudes denotadas mediante T_X(a) suelen ser promedios locales en cajas de una retícula de lado a o variaciones espaciales a una distancia a, coneficientes de ondícula de escala a, etc. Para objetos multifractales, se observa una ley potencial global de escalado de la forma:

al menso en un rango de escalas relevante y para algunos rangos de orden q. Cuando un sistema presenta dicho comportamiento se dice que presenta invariancia de escala, automilaridad o multiescalaridad.

Referencias