- Copo de nieve de Koch
-
Copo de nieve de Koch
Concepción artística de un Copo de Koch
El copo de nieve de Koch es una de las más sencillas figuras fractales, y una de las primeras. Fue inventada por el matemático sueco Helge von Koch en 1906.
Un fractal es un objeto semi geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.
Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.
Construcción
Su construcción es como sigue: Se toma un segmento, se lo divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de π/3 radianes (60 grados). Luego, con los cuatro segmentos, se procede de la misma manera, lo que da 16 segmentos pequeños. Y así sucesivamente, sin nunca parar. La figura representa las seis primeras etapas de la construcción. La última curva es una buena aproximación de la curva final.
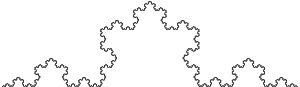
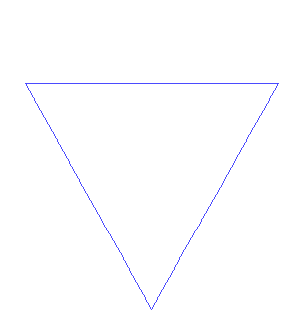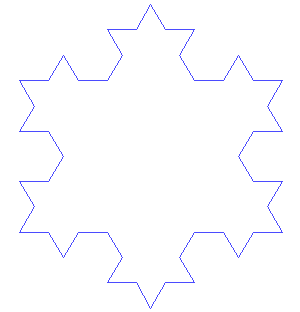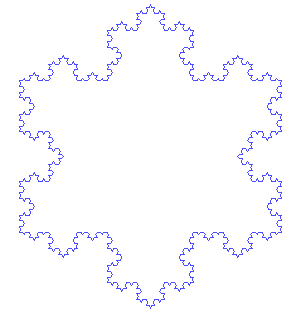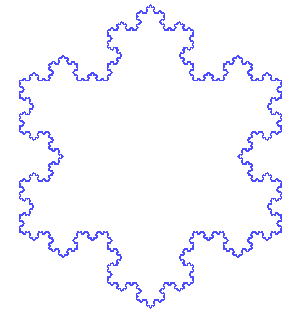
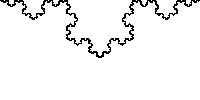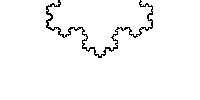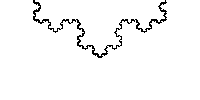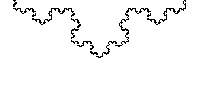Autosimilitud exacta del Copo de nieve de Koch a todas las escalasSi se considera de nuevo la primera figura, notamos que para pasar de una línea a la siguiente se remplaza tres segmentos por cuatro de igual longitud, o sea que la longitud total es multiplicada por 4/3. El límite de la sucesión geométrica de razón 4/3 es infinito, lo que significa que la figura final tiene una longitud infinita (lo que Mandelbrot denomina infinito interno).
Esta característica, típica de los fractales, añadida al hecho que la curva da la impresión de tener cierto espesor a causa de sus constantes cambios de dirección, sugiere que este figura no es unidimensional. Su dimensión tiene que estar entre 1, la de una recta, y 2, la del plano. Para hallarla miremos la última curva: Si agrandamos (mediante una homotecia) tres veces la sección A'B' obtenemos exactamente la sección AB. En la curva final, obtendríamos la sección A'C, es decir cuatro veces la sección inicial.
Se sabe que una homotecia de razón tres multiplica las longitudes por 3, las superficies por 3² = 9, los volúmenes por 3³ = 27, y más generalmente, el "volumen" de objeto de dimensión d por 3d. Entonces tenemos 3d = 4 para el copo de Koch, lo que da: d = ln 4 /ln 3 = 1,26186...
La configuración opuesta-complementaria de un copo de nieve de Koch o copo de nieve fractal suele ser denominada anticopo de nieve.
Véase también
Enlaces externos
Wikimedia Commons alberga contenido multimedia sobre Copo de nieve de Koch.Commons
Categoría: Fractales
Wikimedia foundation. 2010.
