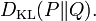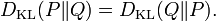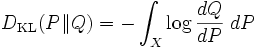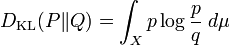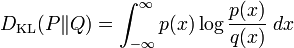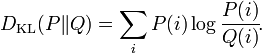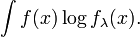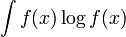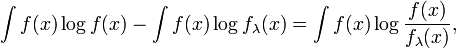Divergencia de Kullback-Leibler

Saltar a navegación, búsqueda

En teoría de la probabilidad la divergencia de Kullback-Leibler es un indicador de la similitud entre dos funciones de distribución. Dentro de la teoría de la información también se la conoce como divergencia de la información, ganancia de la información o entropía relativa.

La divergencia de Kullback-Leibler entre dos funciones de distribución P y Q suele representarse así:

$D_{\mathrm{KL}}(P\|Q).$

Se trata de una divergencia y no una métrica por no ser simétrica, es decir, no siempre se cumple que

$D_{\mathrm{KL}}(P\|Q) = D_{\mathrm{KL}}(Q\|P).$

Contenido

1 Formulación matemática
2 Propiedades
3 Aplicaciones
- 3.1 Teoría de la información
- 3.2 Estadística

Formulación matemática

Si P es una medida de probabilidad es absolutamente continua con respecto a otra, Q, (condición necesaria para que 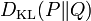$D_{\mathrm{KL}}(P\|Q)$ sea finito) y si 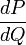$\frac{dP}{dQ}$ es la derivada de Radon–Nikodym de P con respecto a Q, se define la divergencia de Kulllback-Leibler desde P hasta Q de la forma

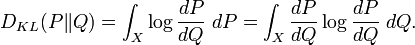$D_{KL}(P\|Q) = \int_X \log \frac{dP}{dQ} \; dP = \int_X \frac{dP}{dQ} \log\frac{dP}{dQ}\; dQ.$ ,

De la misma manera, si Q es absolutamente continua con respecto a P, entonces

$D_{\mathrm{KL}}(P\|Q) = -\int_X \log \frac{d Q}{d P} \; dP \!$

Si ambas medidas son absolutamente continuas con respecto a una tercera medida $μ$ , de forma que $d P = p d μ$ y $d Q = q d μ$ , entonces la fórmula anterior puede reescribirse de la siguiente manera:

$D_{\mathrm{KL}}(P\|Q) = \int_X p \log \frac{p}{q} \;d\mu \!$

La divergencia de Kullback-Leibler no depende de la medida $μ$ . Cuando esta medida es la de medida de Lebesgue sobre el eje real, resulta

$D_{\mathrm{KL}}(P\|Q) = \int_{-\infty}^{\infty} p(x) \log \frac{p(x)}{q(x)} \; dx \!$

y cuando está concentrada sobre un conjunto discreto, se obtiene

$D_{\mathrm{KL}}(P\|Q) = \sum_i P(i) \log \frac{P(i)}{Q(i)} \!.$

Propiedades

Es siempre positiva (puede probarse usando la desigualdad de Jensen).
Es nula si y sólo si P = Q.
No es simétrica (por lo que no se trata de una distancia).

Aplicaciones

Teoría de la información

Los logaritmos en estas fórmulas se toman en base 2 si la información se mide en unidades de bits, o en base e si la información se mide en nats. La mayoría de las fórmulas que involucran la divergencia de Kullback-Leibler son independientes de la base del logaritmo que se tome.

Estadística

En estadística, la divergencia de Kullback-Leibler está íntimamente relacionada con el método de ajuste de distribuciones por máxima verosimilitud. En efecto, si se tienen observaciones $x 1,..., x n$ independientes de una variable aleatoria con función de densidad desconocida f y se tratan de ajustar dentro de una familia de funciones de densidad $f λ$ , de acuerdo con la teoría de la máxima verosimilitud, se busca el parámetro $λ$ que minimiza la función

L_λ =	∑	logf_λ(x_i),
	i

que puede aproximarse (cuando n es grande) por

$\int f(x) \log f_{\lambda} (x ).$

Restando dicha expresión del término constante

$\int f(x) \log f (x )$

se obtiene

$\int f(x) \log f (x ) - \int f(x) \log f_\lambda (x ) = \int f(x) \log \frac {f (x )}{f_\lambda (x )},$

que es la divergencia de Kullback-Leibler entre $f λ$ y la distribución verdadera determinada por f. Es decir, maximizar la función de verosimilitud es (aproximadamente) equivalente a encontrar el parámetro $λ$ que minimiza la divergencia de Kullback-Leibler entre la distribución real y la familia de distribuciones parametrizadas por dicho parámetro.

Obtenido de "Divergencia de Kullback-Leibler"

Categorías: Teoría estadística | Entropía de la información | Probabilidad

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

Distribución normal multivariante — Saltar a navegación, búsqueda Normal multivariante Función de distribución de probabilidad Parámetros (vector real) Σ matriz de covarianza (matriz real definida positiva de dimensión … Wikipedia Español
Máquina de Boltzmann — Una máquina de Boltzmann es un tipo de red neuronal recurrente estocástica. El nombre le fue dado por los investigadores Geoffrey Hinton y Terry Sejnowski. Las máquinas de Boltzmann pueden considerarse como la contrapartida estocástica y… … Wikipedia Español
Alfréd Rényi — (20 de marzo de 1921 – 1 de febrero de 1970) fue un matemático húngaro que hizo importantes contribuciones a la teoría de combinatoria y de teoría de grafos sobre grafos aleatorios.[1] [2] … Wikipedia Español
Desigualdad de Jensen — En matemáticas, la desigualdad de Jensen para funciones convexas relaciona el valor que asigna a una integral con la integral de esa misma función permutando, por así decirlo, la función y la integral. Fue probada por el matemático danés Johan… … Wikipedia Español
Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad … Wikipedia Español
Entropía cruzada — Saltar a navegación, búsqueda En teoría de la información, la entropía cruzada entre dos distribuciones de probabilidad mide la media de bits necesarios para identificar un evento de un conjunto de posibilidades, si un esquema de codificación… … Wikipedia Español
Distribución de Poisson — Saltar a navegación, búsqueda Distribución de Poisson Función de probabilidad El eje horizontal es el índice k. La función solamente está definida en valores enteros de k. Las líneas que conectan los puntos son solo guías para el ojo y no indican … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Divergencia de Kullback-Leibler

Divergencia de Kullback-Leibler

Contenido

Formulación matemática

Propiedades