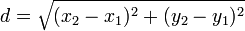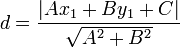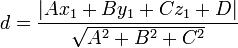- Distancia
-
Distancia
La distancia expresa la proximidad o lejanía entre dos objetos, o el intervalo de tiempo que transcurre entre dos sucesos. También se emplea como expresión para indicar una relación de alejamiento afectivo entre dos personas: el desafecto.
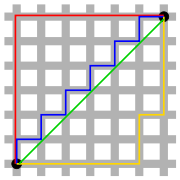
 La menor distancia entre dos puntos recorrida sobre la superficie de una esfera es un arco de círculo máximo: la ortodrómica.
La menor distancia entre dos puntos recorrida sobre la superficie de una esfera es un arco de círculo máximo: la ortodrómica.
En matemática, la distancia entre dos puntos del espacio euclídeo equivale a la longitud del segmento de recta que los une, expresado numéricamente. En espacios más complejos, como los definidos en la geometría no euclidiana, el «camino más corto» entre dos puntos es un segmento de curva.
En física, la distancia es una magnitud escalar, que se expresa en unidades de longitud o tiempo.
Contenido
Distancia en geometría
Se denomina distancia euclídea entre dos puntos A(x1,y1) y B(x2,y2) del plano a la longitud del segmento de recta que tiene por extremos A y B. Puede calcularse así:
La distancia entre un punto P y una recta R es la longitud del segmento de recta que es perpendicular a la recta R:Ax + By + C = 0 y la une al punto P(x1,y1). Puede calcularse así:
donde |·| denota valor absoluto.
La distancia entre dos rectas paralelas es la longitud del segmento de recta perpendicular a ambas que las une.
La distancia entre un punto P y un plano L es la longitud del segmento de recta perpendicular al plano L:Ax + By + Cz + D = 0 que lo une al punto P (x1,y1,z1) y puede calcularse así:
Definición formal
Desde un punto de vista formal, para un conjunto de elementos X se define distancia o métrica como cualquier función binaria d(a,b) de
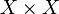 en
en  que verifique las siguientes condiciones:
que verifique las siguientes condiciones:- No negatividad:
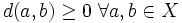
- Simetría:
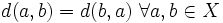
- Desigualdad triangular:
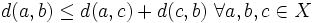
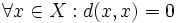 .
.- Si
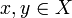 son tales que d(x,y) = 0, entonces x = y.
son tales que d(x,y) = 0, entonces x = y.
Si dejamos de exigir que se cumpla esta última condición, al concepto resultante se le denomina pseudodistancia o pseudométrica.
La distancia es el concepto fundamental de la Topología de Espacios Métricos. Un espacio métrico no es otra cosa que un par (X,d), donde X es un conjunto en el que definimos una distancia d.
En el caso de que tuviéramos un par (X,d) y d fuera una pseudodistancia sobre X, entonces diríamos que tenemos un espacio pseudométrico.
Si (X,d) es un espacio métrico y
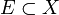 , podemos restringir d a E de la siguiente forma:
, podemos restringir d a E de la siguiente forma: 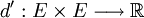 de forma que si
de forma que si 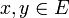 entonces d'(x,y) = d(x,y) (es decir,
entonces d'(x,y) = d(x,y) (es decir, 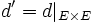 ). La aplicación d' es también una distancia sobre d, y como comparte sobre
). La aplicación d' es también una distancia sobre d, y como comparte sobre 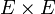 los mismos valores que d, se denota también de la misma manera, es decir, diremos que (E,d) es subespacio métrico de (X,d).
los mismos valores que d, se denota también de la misma manera, es decir, diremos que (E,d) es subespacio métrico de (X,d).Distancia de un punto a un conjunto
Si (X,d) es un espacio métrico,
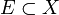 ,
, 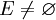 y
y 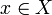 , podemos definir la distancia del punto x al conjunto E de la siguiente manera:
, podemos definir la distancia del punto x al conjunto E de la siguiente manera: 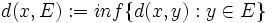 .
.Es de destacar las siguientes tres cosas:
- En primer lugar, en las condiciones dadas, siempre existirá esa distancia, pues d tiene por dominio
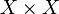 , así que para cualquier
, así que para cualquier 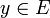 existirá un único valor real positivo d(x,y). Por la completitud de
existirá un único valor real positivo d(x,y). Por la completitud de  y como la imagen de d está acotada inferiormente por 0, queda garantizada la existencia del ínfimo de ese conjunto, esto es, la distancia del punto al conjunto.
y como la imagen de d está acotada inferiormente por 0, queda garantizada la existencia del ínfimo de ese conjunto, esto es, la distancia del punto al conjunto.
- Si
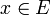 entonces d(x,E) = 0.
entonces d(x,E) = 0.
- Puede ser que d(x,E) = 0 pero
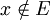 , por ejemplo si x es un punto de adherencia de E. De hecho, la clausura de E es precisamente el conjunto de los puntos de X que tienen distancia 0 a E.
, por ejemplo si x es un punto de adherencia de E. De hecho, la clausura de E es precisamente el conjunto de los puntos de X que tienen distancia 0 a E.
Los casos de distancia de un punto a una recta o de distancia de un punto a un plano no son más que casos particulares de la distancia de un punto a un conjunto, cuando se considera la distancia euclídea.
Distancia entre dos conjuntos
Si (X,d) es un espacio métrico,
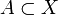 y
y 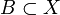 ,
, 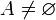 ,
, 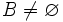 , podemos definir la distancia entre los conjuntos A y B de la siguiente manera:
, podemos definir la distancia entre los conjuntos A y B de la siguiente manera: 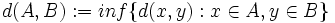 .
.Por la misma razón que antes, siempre está definida. Además d(A,A) = 0, pero puede ocurrir que d(A,B) = 0 y sin embargo
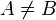 . Es más, podemos tener dos conjuntos cerrados cuya distancia sea 0 y sin embargo sean disjuntos, e incluso que tengan clausuras disjuntas. Por ejemplo, el conjunto
. Es más, podemos tener dos conjuntos cerrados cuya distancia sea 0 y sin embargo sean disjuntos, e incluso que tengan clausuras disjuntas. Por ejemplo, el conjunto 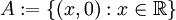 y el conjunto
y el conjunto 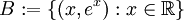 . Por un lado, A = cl(A), B = cl(B) y
. Por un lado, A = cl(A), B = cl(B) y 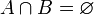 , y por otro d(A,B) = 1.
, y por otro d(A,B) = 1.La distancia entre dos rectas, la distancia entre dos planos, etc. no son más que casos particulares de la distancia entre dos conjuntos cuando se considera la distancia euclídea.
Véase también
- Distancia de Mahalanobis
- Método de los Cuadrantes Centrados en un Punto o Metodo distancia en punto.
Categorías: Geometría | Topología | Matemática elemental
Wikimedia foundation. 2010.