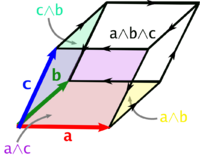
Doble producto vectorial

Doble producto vectorial
Doble producto vectorial de tres vectores a, b y c.

Llamamos doble producto vectorial (o también triple producto vectorial) de tres vectores a la expresión \,\mathbf A \times \left(\mathbf B \times \mathbf C \right)   o  \,\left(\mathbf A \times \mathbf B \right) \times \mathbf C ; esto es, al producto vectorial de dos vectores que se multiplica vectorialmente por un tercer vector.

Contenido

Propiedades

Regla del Chanchito para doble producto vectorial de tres vectores a, b y c.

El producto vectorial de tres vectores a la expresión \, \mathbf A \times \left(\mathbf B \times \mathbf C \right) es un vector contenido en el plano definido por los vectores \mathbf B y \mathbf C, ya que puede demostrarse que se verifica

\, \mathbf A \times \left(\mathbf B \times \mathbf C \right) = \mathbf B \left( \mathbf A \cdot\mathbf C\right)- \mathbf C \left( \mathbf A \cdot\mathbf B\right)

Evidentemente, el producto vectorial no tienen la propiedad asociativa, ya que

\, \left(\mathbf A \times \mathbf B \right)\times \mathbf C = -\mathbf C \times \left(\mathbf A \times \mathbf B \right) = \mathbf B \left( \mathbf A \cdot\mathbf C\right)- \mathbf A \left( \mathbf B \cdot\mathbf C\right)

es un vector contenido en el plano definido por los vectores A y B, por lo que, en general, será

\, \mathbf A \times \left(\mathbf B \times \mathbf C \right) \neq \left(\mathbf A \times \mathbf B \right)\times \mathbf C

resultando fundamental la colocación de los paréntesis.

Identidad de Jacobi: \mathbf a \times (\mathbf b \times \mathbf c ) + \mathbf c \times (\mathbf a \times \mathbf b ) + \mathbf b \times (\mathbf c \times \mathbf a ) = 0

Con la notación de Levi-Civita, el doble producto vectorial se expresa en la forma

\, \mathbf{A} \times (\mathbf{B}\times \mathbf{C}) = \varepsilon_{ijk} A^j \varepsilon_{k\ell m} B^\ell C^m = \varepsilon_{ijk}\varepsilon_{k\ell m} A^j B^\ell C^m

Estas fórmulas son muy útiles a la hora de simplificar un vector en física. Por ejemplo, una igualdad relacionada con los gradientes, y muy útil en el cálculo de vectores es:

\begin{align} \nabla \times (\nabla \times \mathbf{f}) & {}= \nabla (\nabla \cdot \mathbf{f} ) - (\nabla \cdot \nabla) \mathbf{f} \\ & {}= \mbox{grad }(\mbox{div } \mathbf{f} ) - \mbox{laplaciano } \mathbf{f}. \end{align}

Ésto también puede ser considerado como un caso especial del más conocido como operador de Laplace-deRham: Δ = dδ + δd.

Véase también

Referencias

Bibliografía

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Producto vectorial — Saltar a navegación, búsqueda Esquema En álgebra lineal, el producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los d …   Wikipedia Español

  • Producto exterior — En matemática, el producto exterior es una antisimetrización (alternación) del producto tensorial. El producto exterior es una multiplicación asociativa y distributiva de funciones multilineales antisimétrico que sea anticonmutativo para las… …   Wikipedia Español

  • Norma vectorial — Un vector es un elemento de un espacio vectorial del que, en ocasiones, especialmente en Física y Geometría, interesa conocer su longitud. Para ello se hace necesario definir un operador norma que determine la longitud o magnitud del vector bajo… …   Wikipedia Español

  • Vector — Para otros usos de este término, véase Vector (desambiguación). Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio Vectorial. Un vector desde A hasta B. En física, mate …   Wikipedia Español

  • Cuaterniones y rotación en el espacio — Saltar a navegación, búsqueda Los cuaterniones unitarios proporcionan una notación matemática para representar las orientaciones y las rotaciones de objetos en tres dimensiones. Comparados con los ángulos de Euler, son más simples de componer y… …   Wikipedia Español

  • Interacción de canje — Dos orbitales d de iones metálicos vecinos: la interacción de canje J se produce entre dos electrones con el mismo número cuántico de espín Ms, e impide que …   Wikipedia Español

  • Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración …   Wikipedia Español

  • Espacio dual — En matemáticas, la existencia de un espacio vectorial dual refleja de una manera abstracta la relación entre los vectores fila (1×n) y los vectores columna (n×1). La construcción puede darse también para los espacios infinito dimensionales y da… …   Wikipedia Español

  • Mikoyan MiG-29 — MiG 29 Un MiG 29A de la Fuerza Aérea Eslovaca en 1996. Tipo Caza de superioridad aérea Caza polivalente …   Wikipedia Español

  • Integral de superficie — La integral de superficie es una extensión del concepto de integral doble, de igual modo en que la integral de línea es una extensión del concepto de integral de Riemann clásica. Como el nombre lo dice, es aquella integral cuya función es… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”