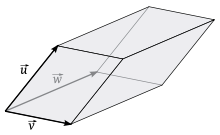
Producto mixto

Producto mixto: El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado escalar.

Contenido

1 Producto punto y producto cruz

2 Triple producto escalar

2.1 Cálculo del triple producto escalar

3 Interpretación geométrica

4 Relaciones cíclicas

5 Véase también

6 Bibliografía

Producto punto y producto cruz

El producto punto es una operación entre dos vectores $\vec{u},\vec{v}$ que da como resultado un número (un escalar) por lo que también se le conoce como producto escalar y está definido como

$\vec{u}\cdot\vec{v} = u_1v_1 + u_2v_2 + \cdots + u_n v_n$ .

Entre sus principales propiedades se encuentra el resultado

$\vec{u}\cdot \vec{v} = |\vec{u}||\vec{v}|\cos \theta$

donde $θ$ es el ángulo que forman los dos vectores. Usando ese resultado es posible establecer el siguiente criterio para determinar si dos vectores son perpendiculares (ortogonales):

Dos vectores $\vec{u},\vec{v}$ son perpendiculares si y sólo si $\vec{u}\cdot\vec{v} = 0$ .

Cuando los vectores son tridimensionales (esto es, son vectores de $\mathbb{R}^3$ ) es posible definir otra multiplicación de vectores cuyo resultado sea también un vector; dicha operación se denomina producto cruz o producto vectorial, definido mediante el determinante

$\vec{u}\times\vec{v} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}$

donde $\vec{i},\vec{j}, \vec{k}$ son los vectores unitarios en la dirección de los tres ejes $x, y, z$ .

El producto $\vec{u}\times\vec{v}$ corresponde a un vector perpendicular a $\vec{u}$ y $\vec{v}$ cuya norma o módulo es

$|\vec{u}\times \vec{v}| = |u||v| \operatorname{sen\,}\theta$ .

donde nuevamente, $θ$ es el ángulo entre los vectores.

Del resultado anterior se deducen dos resultados:

El valor de $|\vec{u}\times\vec{v}|$ es igual al área del paralelogramo determinado por $\vec{u}$ y $\vec{v}$ .

Los vectores $\vec{u}$ y $\vec{v}$ son paralelos (colineales) si y sólo si $\vec{u}\times\vec{v}=0$ .

Observemos la similitud entre este criterio y el de perpendicularidad para el producto punto.

Triple producto escalar

Los triples productos aparecen cuando se desea definir multiplicaciones entre tres vectores. Una expresión de la forma $\vec{u}\cdot\vec{v}\cdot\vec{w}$ no tiene mucho sentido porque el resultado de el primer producto es un escalar

$(\vec{u}\cdot\vec{v})\cdot\vec{w} = r\cdot \vec{w}$

y no es posible calcular el producto punto entre un número (escalar) y un vector.

Sin embargo, cuando los vectores son elementos de $\mathbb{R}^3$ , podemos combinar el producto punto con el producto cruz para definir una nueva operación entre tres vectores que se denomina triple producto escalar pues el resultado será una cantidad escalar. Es importante indicar escalar para diferenciarlo del triple producto vectorial que se obtiene al multiplicar tres vectores usando únicamente el producto cruz y cuyo resultado es, por tanto, un vector.

El triple producto escalar de los vectores $\vec{u},\vec{v},\vec{w}$ se denota por $[\vec{u},\vec{v},\vec{w}]$ y está definido como

$[\vec{u},\vec{v},\vec{w}]=\vec{u}\cdot(\vec{v}\times \vec{w})$

Cálculo del triple producto escalar

Para hallar una fórmula que permita calcular el valor del triple producto escalar a partir de las coordenadas de los vectores procedemos a realizar la sustitución del producto cruz:

$[\vec{u},\vec{v},\vec{w}]$ $~=$ $\vec{u}\cdot(\vec{v}\times\vec{w})$

$~=$ $\vec{u} \cdot \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{vmatrix}$

$~=$ $\vec{u} \cdot \left( \begin{vmatrix}v_2& v_3\\ w_2&w_3\end{vmatrix}\vec{i} -\begin{vmatrix}v_1& v_3\\ w_1&w_3\end{vmatrix}\vec{j} +\begin{vmatrix} v_1& v_2\\ w_1&w_2 \end{vmatrix}\vec{k}\right)$

$~=$ $\begin{vmatrix}v_2& v_3\\ w_2&w_3\end{vmatrix}u_1 -\begin{vmatrix}v_1& v_3\\ w_1&w_3\end{vmatrix}u_2 +\begin{vmatrix} v_1& v_2\\ w_1&w_2 \end{vmatrix}u_3$

en donde hemos usado que

$\vec{u}\cdot \vec{i} = u_1, \vec{u}\cdot \vec{j}=u_2$ y $\vec{u}\cdot\vec{k}= u_3$ .

Sin embargo, la última expresión obtenida es precisamente el desarrollo de un determinante, esto es:

$[\vec{u},\vec{v},\vec{w}] = \begin{vmatrix}u_1 & u_2 & u_3\\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{vmatrix}$

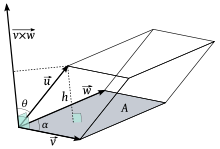
Interpretación geométrica

La similitud que existe entre las fórmulas de determinantes para calcular el producto cruz y el triple producto escalar tienen su paralelo en el siguiente teorema:

Si $\vec{u},\vec{v},\vec{w}$ son vectores tridimensionales, entonces $|\vec{u}\cdot (\vec{v}\times\vec{w})|$ es igual al volumen del paralelepípedo definido por $\vec{u},\vec{v},\vec{w}.$

Paralelepípedo determinado por tres vectores

Así, la norma de un producto cruz representa el valor de un área, mientras que la norma de un triple producto escalar representa un volumen.

La demostración procede observando que

$|\vec{u}\cdot(\vec{v}\times\vec{w})| = |\vec{u}| | \vec{v}\times\vec{w}| |\cos\theta|$

donde $θ$ es el ángulo entre los dos vectores $\vec{u}$ y $\vec{v}\times\vec{w}$ .

Diagrama para demostrar la interpretación geométrica.

Por otro lado $|\vec{v}\times\vec{w}| = |\vec{v}||\vec{w}||\operatorname{sen\,}\alpha|$ corresponde al área del paralelogramo que forman los vectores $\vec{u},\vec{v}$ y $α$ es el ángulo entre ellos.

Así, reordenando los factores el producto tenemos:

$|\vec{u}\cdot(\vec{v}\times\vec{w}) | = (|\vec{u}||\cos\theta|)|\vec{v}\times\vec{w}|=h\cdot A = V.$

donde $h$ es la altura del paralelogramo, como indica la figura, $A$ es el área del paralelogramo de la base y $V$ es el volumen del paralelepípedo.

La intepretación geométrica anterior proporciona un tercer criterio geométrico de estilo similar a los señalados para los otros productos.

Tres vectores $\vec{u},\vec{v},\vec{w}$ son coplanares si y sólo si

$\vec{u}\cdot(\vec{v}\times\vec{w})=0$ .

Lo anterior se sigue de que el volumen del paralelepípedo tendrá volumen cero si y sólo si los vectores que los definen están en un mismo plano (y por tanto tendrá altura cero).

Relaciones cíclicas

A partir de la fórmula de determinante podemos obtener el valor del triple producto escalar cuando los vectores aparecen en distinto orden.

Por ejemplo,

$[\vec{u},\vec{w}, \vec{v}] = \begin{vmatrix} u_1 & u_2 & u_3\\ w_1 & w_2 & w_3 \\ v_1 & v_2 & v_3 \end{vmatrix} = -\begin{vmatrix} u_1 & u_2 & u_3\\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{vmatrix} = - [\vec{u},\vec{v},\vec{w}]$ ,

puesto que intercambiardos filas de un determinante corresponde a cambiar de signo el valor.

En general, intercambiar el orden de dos términos en el triple producto escalar corresponde a un cambio de signo. Realizando esta transposición de términos dos veces regresamos al valor original y así obtenemos la siguiente relación cíclica:

$[\vec{u},\vec{v}, \vec{w}] = [\vec{v},\vec{w}, \vec{u}] = [\vec{w},\vec{u}, \vec{v}]$

Véase también

Producto cruz

Producto punto

Triple producto vectorial

Bibliografía

Ortega, Manuel R. (1989-2006) (en español). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.

Resnick,Robert & Krane, Kenneth S. (2001) (en inglés). Physics. New York: John Wiley & Sons. ISBN 0-471-32057-9.

Categorías:
Cálculo vectorial
Geometría analítica

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Producto de Kronecker — Saltar a navegación, búsqueda En matemáticas, se llama producto de Kronecker, denotado con , a una operación sobre dos matrices de tamaño arbitrario que da como resultado una matriz bloque. Es un caso especial del producto tensorial. El producto… … Wikipedia Español
Producto vectorial — Saltar a navegación, búsqueda Esquema En álgebra lineal, el producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los d … Wikipedia Español
Producto tensorial — Saltar a navegación, búsqueda En matemáticas, el producto tensorial, denotado por , se puede aplicar en diversos contextos a vectores, matrices, tensores y espacios vectoriales. En cada caso la significación del símbolo es la misma: la operación… … Wikipedia Español
Producto escalar — Saltar a navegación, búsqueda En matemáticas el producto escalar, también conocido como producto interno, interior o punto, es una operación definida sobre un espacio vectorial cuyo resultado es una magnitud escalar. Un espacio prehilbertiano es… … Wikipedia Español
Doble producto vectorial — de tres vectores a, b y c. Llamamos doble producto vectorial (o también triple producto vectorial) de tres vectores a la expresión o … Wikipedia Español
Coto Mixto — Saltar a navegación, búsqueda Meaus era un de los tres lugares que formaban el Coto Mixto … Wikipedia Español
Sándwich mixto — Sandwich mixto servido en un plato con su cubertería típica: Tenedor y cuchillo … Wikipedia Español
Sistema Previsional Mixto — El actual Sistema Previsional uruguayo es un Sistema Mixto que se compone de dos tramos de aportación: Contenido 1 El tramo de solidaridad intergeneracional 2 El tramo de ahorro individual 3 Personas comprendidas en el Sistema Mixto … Wikipedia Español
Estado mixto — En mecánica cuántica se llama estado mixto, por contraposición a un estado puro, aquel estado cuántico que no está máximamente intrincado. En otras palabras; si midiéramos más refinadamente los sistemas individuales que forman la colectividad… … Wikipedia Español
Vector — Para otros usos de este término, véase Vector (desambiguación). Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio Vectorial. Un vector desde A hasta B. En física, mate … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Producto mixto

Contenido

Producto punto y producto cruz

Triple producto escalar

Cálculo del triple producto escalar

Interpretación geométrica

Relaciones cíclicas

Véase también

Bibliografía

Mira otros diccionarios:

Compartir el artículo y extractos

$[\vec{u},\vec{v},\vec{w}]$	$~=$	$\vec{u}\cdot(\vec{v}\times\vec{w})$
	$~=$	$\vec{u} \cdot \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{vmatrix}$
	$~=$	$\vec{u} \cdot \left( \begin{vmatrix}v_2& v_3\\ w_2&w_3\end{vmatrix}\vec{i} -\begin{vmatrix}v_1& v_3\\ w_1&w_3\end{vmatrix}\vec{j} +\begin{vmatrix} v_1& v_2\\ w_1&w_2 \end{vmatrix}\vec{k}\right)$
	$~=$	$\begin{vmatrix}v_2& v_3\\ w_2&w_3\end{vmatrix}u_1 -\begin{vmatrix}v_1& v_3\\ w_1&w_3\end{vmatrix}u_2 +\begin{vmatrix} v_1& v_2\\ w_1&w_2 \end{vmatrix}u_3$

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Producto mixto

Contenido

Producto punto y producto cruz

Triple producto escalar

Cálculo del triple producto escalar

Interpretación geométrica

Relaciones cíclicas

Véase también

Bibliografía

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo