Dominio de ideales principales
- Dominio de ideales principales
-
Dominio de ideales principales
Un dominio de ideales principales (DIP) es un dominio de integridad en el que todo ideal es principal (está generado por un sólo elemento). Cualquier dominio de ideales principales es también un dominio de factorización única, pero no al revés. En estos dominios existe siempre el máximo común divisor y el mínimo común múltiplo, hecho que no ocurre en los dominios de integridad en general. El máximo común divisor de a y b en un DIP es el elemento d del anillo tal que <a,b>=<d>.
Ejemplos
El anillo 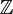 de los números enteros es un ejemplo de dominio de ideales principales.
de los números enteros es un ejemplo de dominio de ideales principales.
Si k es un cuerpo y k[X,Y] es su anillo de polinomios en dos variables, entonces k[X,Y] es un dominio de factorización única que no es dominio de ideales principales.
Categoría: Teoría de anillos
Wikimedia foundation.
2010.
Mira otros diccionarios:
Dominio de integridad — Saltar a navegación, búsqueda Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en… … Wikipedia Español
Dominio — Saltar a navegación, búsqueda El término dominio puede referirse a: Dominio (biología), una subdivisión de los seres vivos; Dominio (teología), un dogma eclesiástico basado en el Génesis (1:20 28); Dominio (redes informáticas); Dominio de… … Wikipedia Español
Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… … Wikipedia Español
Generador de un ideal — Sea A un dominio y X un subconjunto de A. Si I es el mínimo ideal de A tal que , se dice que X es el generador del ideal I o, equivalentemente, que I es un ideal de A generado por X. El ideal de A … Wikipedia Español
Anillo de polinomios — Saltar a navegación, búsqueda Sea A un anillo y S cualquier conjunto. El conjunto A[S] de todos los objetos (1) , en donde … Wikipedia Español
Ideal principal — Este artículo está huérfano, pues pocos o ningún artículo enlazan aquí. Por favor, introduce enlaces hacia esta página desde otros artículos relacionados … Wikipedia Español
Lema de Gauss — En la teoría de polinomios, el lema de Gauss, o Criterio de la irreducibilidad de Gauss, afirma que si es un dominio de factorización única (DFU) y es su cuerpo de cocientes (o cuerpo de fracciones), entonces el contenido de dos polinomios dados… … Wikipedia Español
Identidad de Bézout — La identidad de Bézout o Lema de Bézout enuncia que si a y b son números enteros con máximo común divisor d, entonces existen enteros x e y tales que Los números x e y pueden determinarse mediante el algoritmo extendido de Euclides, pero no se… … Wikipedia Español
Módulo inyectivo — En matemáticas, un módulo inyectivo es un módulo Q que comparte ciertas propiedades deseables con el Z módulo Q de todos los números racionales. Específicamente, si Q es un submódulo de algún otro módulo, entonces es un sumando directo de ese… … Wikipedia Español
Identidad de Bézout — La identidad de Bézout enuncia que si a y b son números enteros con máximo común divisor d, entonces existen enteros x e y tales que ax + by = d Los números x e y pueden determinarse mediante el … Enciclopedia Universal
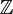 de los números enteros es un ejemplo de dominio de ideales principales.
de los números enteros es un ejemplo de dominio de ideales principales.