Ley de Biot-Savart

Ley de Biot-Savart
Ilustración de la ecuación de Biot-Savart.

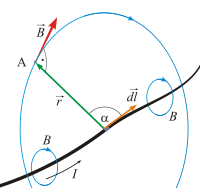
La ley de Biot-Savart indica el campo magnético creado por corrientes eléctricas estacionarias.

En el caso de las corrientes que circulan por circuitos filiformes (o cerrados), la contribución de un elemento infinitesimal de longitud d\vec l del circuito recorrido por una corriente I \, crea una contribución elemental de campo magnético, d\vec B, en el punto situado en la posición que apunta el vector \vec Ur a una distancia r respecto de d\vec l, quien apunta en dirección a la corriente I:

d\vec B = \frac{\mu_0}{4\pi} \frac{I d\vec l \times \hat{r}}{r^2}

donde μ0 es la permeabilidad magnética del vacío, y \hat{r} es un vector unitario.


En el caso de corrientes distribuidas en volúmenes, la contribución de cada elemento de volumen de la distribución, viene dado por

d\vec B = \frac{\mu_0}{4\pi} \frac{\vec J \times \vec R}{r^3} dv

donde \vec{J} es la densidad de corriente en el elemento de volumen dv \, y \vec{R} es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.


En ambos casos, el campo final resulta de aplicar el principio de superposición a través de la expresión

\vec B = \int d\vec{B}

En la que la integral se extiende a todo el recinto que contiene las fuentes del campo.

La ley de Biot-Savart es fundamental en magnetostática tanto como la ley de Coulomb lo es en electrostática.


Contenido

Ley de Biot-Savart generalizada

En una aproximación magnetostática, el campo magnético puede ser determinado si se conoce la densidad de corriente j:

\mathbf{B}= K_m\int{\frac{\mathbf{j} \times \mathbf{\hat r}}{r^2}dV}

donde:

\ dV es el elemento diferencial de volumen.
K_m = \frac{\mu_0}{4\pi} es la constante magnética.

Divergencia y rotacional de \vec B a partir de la ley de Biot y Savart

La divergencia y rotacional de un campo magnético estacionario puede hallarse por simple aplicación de tales operadores a la ley de Biot y Savart

Divergencia

Aplicando el operador gradiente a la expresión tenemos:

\nabla \cdot \vec B=\frac {\mu_0}{4\pi}\int_V \nabla\cdot(\vec J \times \frac{\hat r}{r^2})dV'

Dado que la divergencia se aplica en un punto de evaluación del campo independiente de la integración de \vec J en todo el volumen, el operador no afecta a \vec J . Aplicando la correspondiente identidad vectorial:

\nabla \cdot \vec B=-\frac {\mu_0}{4\pi}\int_V \vec J \cdot (\nabla \times (\nabla\cdot\frac{1}{r}))dV'

Dado que:

(\nabla \times (\nabla\cdot\frac{1}{r}))=0

Tenemos:

\nabla\cdot\vec B=0

Rotacional

Aplicando el operador rotacional tenemos:

\nabla \times \vec B=\frac {\mu_0}{4\pi}\int_V \nabla\times(\vec J \times \frac{\hat r}{r^2})dV'

Al igual que ocurría en la divergencia, el operador no afecta a \vec J ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que \nabla\cdot\frac{\hat r}{r^2}=4\pi\cdot\delta (r)

\nabla \times \vec B=\frac {\mu_0}{4\pi}\int_V \vec J \cdot(\nabla\cdot \frac{\hat r}{r^2})dV'=\mu_0\int_V \vec J\cdot\delta (r) \cdot dV'

Realizando la integración obtenemos finalmente:

\nabla \times \vec B=\mu_0\cdot\vec J

Nótese que el resultado anterior sólo es válido para campos magnéticos estacionarios. Si el campo magnético no fuese estacionario aparecería aparte el término debido a la corriente de desplazamiento.


Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Ley de Biot-Savart — La ley de Biot Savart indica el campo magnético creado por una densidad de corriente constante. En particular, un elemento infinitesimal de longitud recorrido por una corriente crea un campo magnético situado en la posición respecto de : donde es …   Enciclopedia Universal

  • Savart — En acústica musical, el savart es una medida logarítmica de afinación musical. Corresponde aproximadamente a la cantidad de desafinación que puede percibir un músico bien entrenado (unos 4 cents). Su nombre proviene del físico y médico francés… …   Wikipedia Español

  • Biot, Jean-Baptiste — ► (1774 1862) Físico francés. Estableció diversas teorías entre las que destacan la de la conductibilidad calorífica. Formuló la llamada ley de Biot y Savart …   Enciclopedia Universal

  • Félix Savart — Violín trapezoidal de Savart. Ilustración de la ecuación Biot Savart Guedelhoefer …   Wikipedia Español

  • Jean Baptiste Biot — Jean Baptiste Biott. Jean Baptiste Biott fue un físico, astrónomo y matemático francés. Nació el 21 de abril de 1774, en París y falleció el 3 de febrero de 1862 en la misma ciudad. Obra Jean Baptiste Biott fue la primera per …   Wikipedia Español

  • Biot y Savart — Biot y Savart, ley de …   Enciclopedia Universal

  • Biot y Savart, ley de — ► ELECTROMAGNETISMO Ley formulada por J.B. Biot y F. Savart, según la cual una corriente de intensidad I que circula por un conductor rectilíneo crea a su alrededor un campo magnético directamente proporcional a I e inversamente proporcional a la …   Enciclopedia Universal

  • Savart, Félix — ► (1791 1841) Físico francés. En colaboración con Biot, descubrió la ley que lleva el nombre de ambos. (V. Biot.) …   Enciclopedia Universal

  • Electromagnetismo — Ferrofluido que se agrupa cerca de los polos de un magneto poderoso. El electromagnetismo es una rama de la física …   Wikipedia Español

  • Sistema Cegesimal de Unidades — El sistema cegesimal de unidades, también llamado sistema CGS, es un sistema de unidades basado en el centímetro, el gramo y el segundo. Su nombre es el acrónimo de estas tres unidades. El sistema CGS ha sido casi totalmente reemplazado por el… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”