- Ecuación de Debye-Huckel
-
Ecuación de Debye-Huckel
Peter Debye y Erich Hückel plantearon un modelo que describe una mezcla de iones (electrolitos), inmersos en un medio dieléctrico continuo de temperatura T, presión P y concentración molar ci, , en donde los iones de diferente tipo se denotan como i. Las consideraciones retomadas por Debye y Huckel se basan en que las únicas interacciones presentes en ese medio son las electrostáticas.
El medio en el que los electrolitos están inmersos es un dieléctrico continuo sin tener en cuenta una estructura molecular que pertenezca a ella, con constante dieléctrica ε0, que es dependiente de la temperatura y la presión.• Los iones son del tipo Van der Waals, esféricos e impenetrables no polarizables, de radio ai(tipo i) y carga eléctrica zi, sometidos a una campo eléctrico de simetría esférica con un potencial eléctrico
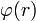 .
.La energía de interacción electrostática es pequeña comparada con la energía térmica:
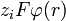 mayor que RT y además todos los electrolitos están disociados.
mayor que RT y además todos los electrolitos están disociados.Las condiciones de contorno se presentan por las siguientes consideraciones:
- El sistema (soluto y electrolitos) es eléctricamente neutro.
- El valor medio temporal de la densidad de carga eléctrica ρ es nula en cualquier diferencial de volumen dV, además su potencial eléctrico también es nulo respecto a otro diferencial de volumen.
- Alrededor de una carga denotada como el ion central j, estará rodeada por valores medios temporales de densidad de carga ρ(j) y
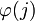 finitos no nulos los cuales alrededor de la carga central j predominarán los valores de carga de signo contrario a j. Por tanto la simetría esférica y la electroneutralidad llevan a escribir lo siguiente:
finitos no nulos los cuales alrededor de la carga central j predominarán los valores de carga de signo contrario a j. Por tanto la simetría esférica y la electroneutralidad llevan a escribir lo siguiente: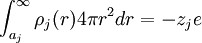
- Se puede involucrar la ecuación de Poisson debido a que las cargas son estáticas.
Ya asumidas las condiciones de contorno y las consideraciones podemos plantear el procedimiento ubicándonos en el ion central j, observando que debido a las interacciones electrostáticas, una distribución radial no uniforme de la densidad numérica ni(r) (=Na ci)de las distintas especies iónicas (i) presentes alrededor de la carga j.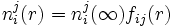
donde
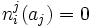
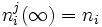 fij(aj) = 0
fij(aj) = 0 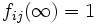
Donde fij es un factor de proporcionalidad denotado como
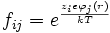
del tipo distribución de Boltzmann que denota la dependencia del factor con la energía.
Por tanto para la densidad de carga alrededor del ion central:
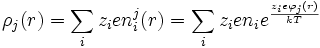
Por la condición de que la energía térmica es mucho mayor de la energía de interacción:
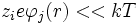
lo que permite desarrollar en serie:
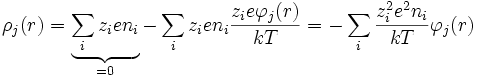
Debye y Huckel definieron un parámetro llamado la longitud de Debye-Huckel que posee unidades de longitud inverso:
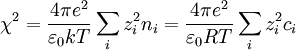
Por tanto la expresión que Debye y Huckel reescriben es:
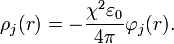
La segunda parte es reemplazar el resultado anterior en la ecuación de Poisson-Boltzmann, definida como:
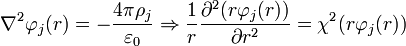
La solución para este tipo de ecuaciones es de la forma:
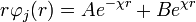
Teniendo en cuenta que para
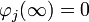 , entonces B=0 y la ecuación anterior queda:
, entonces B=0 y la ecuación anterior queda: 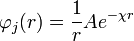
La expresión anterior se conoce como la expresión genérica del potencial de Debye-Huckel, para encontrar el valor de la constante A se reemplaza la anterior expresión en la expresión de Debye-Huckel, y luego este resultado en la integral planteada al inicio, el resultado es:
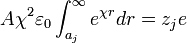
Integrando por partes se obtiene A como:
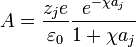
Por tanto la forma del potencial de Debye–Huckel queda de la forma:
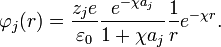 Categoría: Física
Categoría: Física
Wikimedia foundation. 2010.
