Ecuación de Jacobi

Ecuación de Jacobi

Ecuación de Jacobi

La ecuación de Jacobi es una ecuación diferencial de la forma:

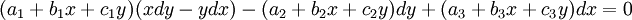
(a_1+b_1x+c_1y)(xdy-ydx)-(a_2+b_2x+c_2y)dy+(a_3+b_3x+c_3y)dx=0 \,

Con coeficientes reales. La ecuación de Jacobi tiene al menos una solución de la forma

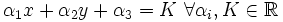
\alpha_1x+\alpha_2y+\alpha_3=K \ \forall \alpha_i, K \in \mathbb R

Sea la matriz

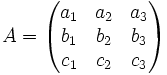
A=\begin{pmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{pmatrix}

Entonces, si el espectro de A (conjunto de autovalores de A) es

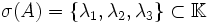
\sigma(A)=\{\lambda_1, \lambda_2, \lambda_3 \} \subset \mathbb K

Y los autovalores son distintos dos a dos, definimos los coeficientes ki como las soluciones del sistema

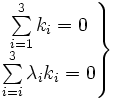
\left.\begin{matrix} \sum\limits_{i=1}^3 k_i = 0 \\ \sum\limits_{i=i}^3 \lambda_i k_i =0 \end{matrix}\right\}

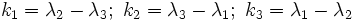
Por lo tanto los coeficientes son k_1=\lambda_2 -\lambda_3; \ k_2=\lambda_3 - \lambda_1; \ k_3=\lambda_1 - \lambda_2

Sea ahora la función implícita

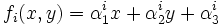
f_i(x,y)=\alpha_1^i x +\alpha_2^i y +\alpha_3^i

La solución de la ecuación de Jacobi dada por el autovalor λi tal que los coeficientes 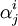\alpha_j^i quedan definidos por el sistema en forma matricial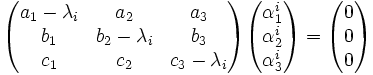

\begin{pmatrix} a_1 -\lambda_i& a_2 & a_3 \\ b_1 & b_2 -\lambda_i& b_3 \\ c_1 & c_2 & c_3-\lambda_i \\ \end{pmatrix} \begin{pmatrix} \alpha_1^i \\ \alpha_2^i \\ \alpha_3^i \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}

Entonces la solución general de la ecuación de Jacobi viene dada por

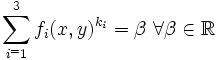\sum\limits_{i^=1}^3 f_i(x,y)^{k_i} = \beta \ \forall \beta \in \mathbb R

Obtenido de "Ecuaci%C3%B3n de Jacobi"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Ecuación diferencial — Saltar a navegación, búsqueda Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se… …   Wikipedia Español

  • Ecuación de Hamilton-Jacobi — Saltar a navegación, búsqueda La ecuación de Hamilton Jacobi es una ecuación diferencial en derivadas parciales usada en mecánica clásica y mecánica relativista que permite encontrar las ecuaciones de evolución temporal o de movimiento . La… …   Wikipedia Español

  • Ecuación de Schrödinger — Saltar a navegación, búsqueda La ecuación de Schrödinger fue desarrollada por el físico austríaco Erwin Schrödinger en 1925. Describe la evolución temporal de una partícula masiva no relativista. Es de importancia central en la teoría de la… …   Wikipedia Español

  • Ecuación de la Eikonal — Saltar a navegación, búsqueda La Ecuación Eikonal es una Ecuación en derivadas parciales con no linealidad encontrada en propagación de ondas, cuando la ecuacion de onda es aproximada usando la Teoría WKB. Esto es derivable desde las Ecuaciones… …   Wikipedia Español

  • Ecuación en derivadas parciales — Saltar a navegación, búsqueda En matemáticas una ecuación en derivadas parciales (a veces abreviado como EDP) es una relación entre una función u de varias variables independientes x,y,z,t,... y las derivadas parciales de u respecto de esas… …   Wikipedia Español

  • Ecuación de quinto grado — Saltar a navegación, búsqueda Polinomio de 5º grado: f(x) = (x+4)(x+2)(x+1)(x 1)(x 3)/20+2 En matemática, se denomina ecuación quíntica o de quinto grado a una ecuación polinómica en que el exponente de la variable independiente de mayor grado es …   Wikipedia Español

  • Ecuación de Korteweg-de Vries — Saltar a navegación, búsqueda La ecuación de Korteweg de Vries o KdV es una ecuación en derivadas parciales que incluye efectos de no linealidad y dispersión a la vez. Físicamente es un modelo que describe, en una dimensión espacial, la… …   Wikipedia Español

  • Carl Gustav Jakob Jacobi — Saltar a navegación, búsqueda Karl Gustav Jacob Jacobi Carl Gustav Jakob Jacobi (n. 10 de diciembre de 1804 en Potsdam, Prusia, actual Alemania, † 18 de febrero de 1851 en Berlín) …   Wikipedia Español

  • Método de Jacobi — En análisis numérico el método de Jacobi es un método iterativo, usado para resolver sistemas de ecuaciones lineales del tipo Ax = b. El algoritmo toma su nombre del matemático alemán Carl Gustav Jakob Jacobi. El método de Jacobi consiste en usar …   Wikipedia Español

  • Identidad de Jacobi — Este artículo o sección tiene un estilo difícil de entender para lectores que no son expertos en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”