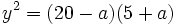En matemática, se denomina ecuación quíntica o de quinto grado a una ecuación polinómica en que el exponente de la variable independiente de mayor grado es cinco. Es de la forma general:

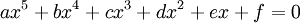
donde a, b, c, d, e y f son miembros de un cuerpo (habitualmente el de los números racionales, el de los reales o los complejos), y .

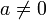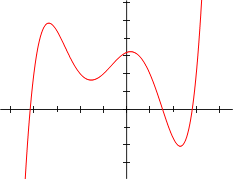
Debido a que son de grado impar, la gráfica de las funciones quínticas normales se parece a la de las funciones cúbicas normales, excepto en que pueden poseer un máximo y un mínimo locales adicionales. La derivada de una función quíntica es una función cuártica.

Contenido 1 Búsqueda de raíces de una ecuación quíntica 1.1 Factorización de radicales 1.2 Otros métodos analíticos 1.3 Métodos numéricos 2 Referencias 3 Véase también 4 Enlaces externos

Búsqueda de raíces de una ecuación quíntica

Encontrar las raíces de un polinomio (valores de x que satisfacen tal ecuación) en el caso racional dados sus coeficientes ha sido un importante problema matemático.

La resolución de ecuaciones lineales, cuadráticas, cúbicas y cuárticas mediante factorización de raíces es bastante sencilla cuando las raíces son racionales o reales; también hay fórmulas que proporcionan las soluciones. Sin embargo, no hay una fórmula general en términos de raíces para las ecuaciones de quinto grado sobre los racionales; mediante un número finito de sumas, restas, multiplicaciones, divisiones y extracciones de raíces. Esto lo probó por primera vez el teorema de Abel-Ruffini, publicado en 1824, que fue una de las primeras aplicaciones de la teoría de grupos en el álgebra. Este resultado también se cumple para ecuaciones de mayor grado.

Factorización de radicales

Algunas ecuaciones de quinto grado se pueden resolver mediante factorización de radicales, como por ejemplo x⁵ − x⁴ − x + 1 = 0, que puede escribirse como (x² + 1)(x + 1)(x − 1)² = 0. Otras quínticas como x⁵ − x + 1 = 0 no pueden factorizarse de manera sencilla. Évariste Galois desarrolló técnicas para determinar si una ecuación dada podría ser resuelta mediante factorización, lo que dio pie al campo de la teoría de Galois. Usando la teoría de Galois, John Stuart Glashan, George Paxton Young y Carl Runge mostraron en 1885 que cualquier quíntica resoluble irreducible en forma de Bring-Jerrard,

x⁵ + ax + b = 0

debe forzosamente tener la siguiente forma:

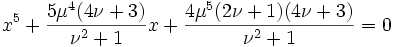
donde μ y ν son racionales. En 1994, Spearman y Williams dieron una alternativa,

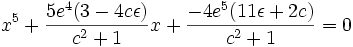
con 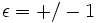. Dado que haciendo un uso juicioso de las transformaciones de Tschirnhaus se puede convertir una quíntica a forma de Bring-Jerrard, esto da una condición necesaria y suficiente para que se pueda resolver mediante raíces. La relación entre las parametrizaciones de 1885 y 1994 puede verse definiendo la expresión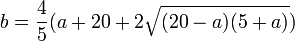

donde

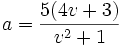
y obtenemos la primera parametrización usando el caso negativo de la raíz cuadrada, mientras que el caso positivo nos da la segunda con ε = − 1. Por tanto esto es una condición necesaria (pero no suficiente) para que la quíntica resoluble irreducible

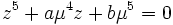
con coeficientes racionales debe satisfacer la curva cuadrática simple

siendo a e y racionales.

Otros métodos analíticos

También existen otros métodos para resolver quínticas. Jerrard mostró alrededor de 1835 que las quínticas se pueden resolver usando ultraradicales (también conocidos como radicales de Bring), las raíces reales de t⁵ + t − a siendo a un número real. En 1858 Charles Hermite mostró que el radical de Bring se podía caracterizar en términos de las funciones theta de Jacobi y sus funciones modulares elípticas asociadas, usando un enfoque similar al más familiar usado al resolver ecuaciones cúbicas mediante funciones trigonométricas. Leopold Kronecker desarrolló una manera más sencilla de derivar el resultado de Hermite usando Teoría de grupos, prácticamente al mismo tiempo que Francesco Brioschi. Más adelante, Felix Klein llegó a un método particularmente elegante que relaciona las simetrías del icosaedro, la teoría de Galois y las funciones modulares elípticas que aparecen en la solución de Hermite, dando una explicación de por qué deben aparecer, y desarrolló su propia solución en términos de las funciones hipergeométricas generalizadas. El mexicano Graciano Ricalde Gamboa descubrió un método para la resolución de la ecuación de quinto grado mediante el uso de funciones elípticas

Métodos numéricos

Los métodos numéricos como el método de Newton-Raphson o de prueba y error dan resultados muy rápidamente si sólo se necesitan valores aproximados para las raíces, o si se sabe que las soluciones comprenden sólo expresiones sencillas (como en exámenes). También se pueden usar otros métodos como el de Laguerre o el de Jenkins-Traub para encontrar numéricamente las raíces de una quíntica de forma más fiable.

Referencias

• Charles Hermite, "Sur la Résolution de L'Equation Du Cinquème Degré" (1858) en Œuvres de Charles Hermite, t.2, pp. 5-21, Gauthier-Villars, 1908.
• Felix Klein, Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree, trad. George Gavin Morrice, Trübner & Co., 1888. ISBN 0-486-49528-0.
• Ian Stewart, Galois Theory 2nd Edition, Chapman and Hall, 1989. ISBN 0-412-34550-1. Comenta la Teoría de Galois en general incluyendo una prueba de la no resolubilidad de la quíntica general.

Véase también

• Ecuación
• Ecuación de segundo grado
• Ecuación de tercer grado
• Ecuación de cuarto grado
• Ecuaciones con radicales
• Grupo resoluble
• Teoría de ecuaciones
• Niels Henrik Abel
• Portal:Matemática Contenido relacionado con Matemática.

Enlaces externos

• Mathworld - Quintic Equation - más detalles sobre métodos para resolver quínticas.
• Solving the Quintic with Mathematica - póster sobre las soluciones para quínticas
• Lectures on the Icosahedron - El libro de Klein está disponible en línea