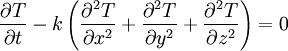Ecuación del calor

Ecuación del calor

Ecuación del calor

La ecuación del calor predice que si un cuerpo a una temperatura T se sumerge en una caja con agua a menor temperatura, la temperatura del cuerpo disminuirá, y finalmente (teóricamente después de un tiempo infinito, y siempre que no existan fuentes de calor externas) la temperatura del cuerpo y la del agua serán iguales (estarán en equilibrio térmico).

La ecuación del calor es una importante ecuación diferencial en derivadas parciales que describe la distribución del calor (o variaciones de la temperatura) en una región a lo largo del transcurso del tiempo. Para el caso de una función de tres variables en el espacio (x,y,z) y la variable temporal t, la ecuación del calor es

\frac{\partial T}{\partial t} -k\left(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}+\frac{\partial^2T}{\partial z^2}\right)=0

donde k es una constante.

La ecuación del calor es de una importancia fundamental en numerosos y diversos campos de la ciencia. En las matemáticas, es las ecuaciones parabólicas en derivadas parciales por antonomasia. En la estadística, la ecuación del calor está vinculada con el estudio del movimiento browniano a través de la ecuación de Fokker–Planck. La ecuación de difusión, es una versión más general de la ecuación del calor, y se relaciona principalmente con el estudio de procesos de difusión química.

Contenido

Véase también

  • Heat kernel regularization
  • Caloric polynomial
  • Neher–McGrath


Notas


Referencias

  • Cannon, John (1984), The One-Dimensional Heat Equation, Encyclopedia of mathematics and its applications, Addison-Wesley, ISBN 0-521-30243-9 


  • Crank, J.; Nicolson, P. (1947), "A Practical Method for Numerical Evaluation of Solutions of Partial Differential Equations of the Heat-Conduction Type", Proceedings of the Cambridge Philosophical Society 43: 50-67 


  • Einstein, A (1905), "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen", Ann. Phys. Leipzig 17: 549-560 


  • Evans, L.C. (1998), Partial Differential Equations, American Mathematical Society, ISBN 0-8218-0772-2 


  • John, Fritz (1991), Partial Differential Equations (4th ed. edición), Springer, ISBN 978-0387906096 


  • Wilmott, P.; Howison, S.; Dewynne, J. (1995), The Mathematics of Financial Derivatives:A Student Introduction, Cambridge University Press 


Enlaces externos

Commons

Obtenido de "Ecuaci%C3%B3n del calor"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuación del cohete de Tsiolskovski — Saltar a navegación, búsqueda La ecuación del cohete de Tsiolkovski, llamada así por Konstantín Tsiolkovski que fue el primero que la derivó, considera el principio del cohete: un aparato que puede aplicar aceleración al mismo (empuje) expulsando …   Wikipedia Español

  • ecuación diferencial parcial — En matemática, una ecuación que contiene derivadas parciales, y que expresa un proceso de cambio que depende de más de una variable independiente. Puede ser leída como una afirmación sobre cómo evoluciona un proceso sin especificar la función… …   Enciclopedia Universal

  • Calor y trabajo — Saltar a navegación, búsqueda Contenido 1 Primer principio de la termodinámica 2 La energía interna como función de la temperatura 3 Calor molar a volumen constante …   Wikipedia Español

  • Ecuación en derivadas parciales — Saltar a navegación, búsqueda En matemáticas una ecuación en derivadas parciales (a veces abreviado como EDP) es una relación entre una función u de varias variables independientes x,y,z,t,... y las derivadas parciales de u respecto de esas… …   Wikipedia Español

  • Ecuación de la Eikonal — Saltar a navegación, búsqueda La Ecuación Eikonal es una Ecuación en derivadas parciales con no linealidad encontrada en propagación de ondas, cuando la ecuacion de onda es aproximada usando la Teoría WKB. Esto es derivable desde las Ecuaciones… …   Wikipedia Español

  • Calor y rendimiento muscular — Saltar a navegación, búsqueda Los músculos son estructuras contráctiles que le permiten a una gran cantidad de seres vivos su movilización y la realización de muchas de sus tareas en la vida diaria. La manera de hacer esto posible es realizando… …   Wikipedia Español

  • Ecuación parabólica en derivadas parciales — Saltar a navegación, búsqueda Una ecuación parabólica en derivadas parciales es una ecuación diferencial parcial de segundo orden del tipo en la cual la matriz tiene un determinante igual a 0. Algunos ejemplo de ecuaciones diferenciales parciales …   Wikipedia Español

  • Ecuación constitutiva — Saltar a navegación, búsqueda Una ecuación constitutiva es una relación entre las variables termodinámicas y/o mecánicas de un sistema físico: presión, volumen, tensión, deformación, temperatura, densidad, entropía, etc. Cada material o… …   Wikipedia Español

  • Programa del transbordador espacial — Este artículo se refiere a los transbordadores espaciales estadounidenses. Existió un proyecto cancelado de transbordador espacial ruso, cuyas características pueden consultarse en Transbordador Buran, y otro proyecto cancelado de transbordador… …   Wikipedia Español

  • Anexo:Ganadores del Premio Nobel de Física — El Premio Nobel de Física fue establecido en el testamento de 1895 del químico sueco Alfred Nobel. El Premio Nobel de Física …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”