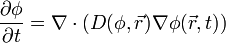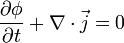Ecuación de difusión

Ecuación de difusión

Ecuación de difusión

La ecuación de la difusión es una ecuación en derivadas parciales que describe fluctuaciones de densidad en un material que se difunde. Es también usada para describir procesos exhibiendo un comportamiento de difusión.

Contenido

Ecuación

La ecuación es generalmente escrita como:

\frac{\partial\phi}{\partial t}=\nabla\cdot (D(\phi,\vec{r})\nabla\phi(\vec{r},t))

donde φ es la densidad del material que difunde, t es tiempo, y D es el coeficiente de difusión colectivo, 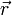\vec{r} es la coordenada espacial y el símbolo nabla (∇) representa el vector operador diferencial nabla. Si el coeficiente de difusón depende de la densidad, entonces la ecuación no es lineal; de otra manera sería lineal. Si D es constante, entonces la ecuación se reduce a la siguiente ecuación lineal:

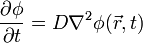\frac{\partial\phi}{\partial t}=D\nabla^2\phi(\vec{r},t),

Más generalmente, cuando D es una matriz simétrica definida positiva, la ecuación describe una difusión anisótropa.

Derivación

La ecuación de difusión puede deducirse a partir de la ecuación de continuidad. La misma expresa que un cambio en densidad en un sistema es debido a un flujo entrante o a un flujo saliente de material del sistema. O sea no puede haber ni creación ni destrucción de materia.

\frac{\partial\phi}{\partial t}+\nabla\cdot\vec{j}=0

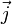donde \vec{j} es el flujo del material que difunde. La ecuación de difusión puede ser obtenida fácilmente de esta relación cuando se la combina con la Ley de Fick, que asume que el flujo del material que difunde en cualquier parte del sistema es proporcional al gradiente local de densidad:

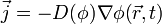\vec{j}=-D(\phi)\nabla\phi(\vec{r},t).

Véase también

Enlaces externos

Obtenido de "Ecuaci%C3%B3n de difusi%C3%B3n"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Difusión simple a través de la membrana celular — Saltar a navegación, búsqueda La célula está cubierta por una superficie externa, conformada principalmente por fosfolípidos y proteínas, denominada membrana celular. Su función es proteger e intermediar en el proceso de transporte de moléculas y …   Wikipedia Español

  • Ecuación del calor — Saltar a navegación, búsqueda La ecuación del calor predice que si un cuerpo a una temperatura T se sumerge en una caja con agua a menor temperatura, la temperatura del cuerpo disminuirá, y finalmente (teóricamente después de un tiempo infinito,… …   Wikipedia Español

  • Ecuación de Fokker-Planck — Saltar a navegación, búsqueda La ecuación de Fokker–Planck, denominada así por Adriaan Fokker y Max Planck, y también conocida como ecuación avanzada de Kolmogórov (por Andréi Kolmogórov), describe la evolución temporal de la función de densidad… …   Wikipedia Español

  • Ecuación de Mason-Weaver — Saltar a navegación, búsqueda La ecuación de Mason Weaver describe la sedimentación y difusión de solutos bajo la acción de una fuerza uniforme, usualmente el campo gravitatorio.[1] Suponiendo que el campo gravitatorio se aline en la dirección z… …   Wikipedia Español

  • Ecuación de onda — Saltar a navegación, búsqueda La ecuación de onda es una importante ecuación diferencial parcial lineal de segundo orden que describe la propagación de una variedad de ondas, como las ondas sonoras, las ondas de luz y las ondas en el agua. Es… …   Wikipedia Español

  • Ecuación en derivadas parciales — Saltar a navegación, búsqueda En matemáticas una ecuación en derivadas parciales (a veces abreviado como EDP) es una relación entre una función u de varias variables independientes x,y,z,t,... y las derivadas parciales de u respecto de esas… …   Wikipedia Español

  • Difusión — Saltar a navegación, búsqueda Para otros usos de este término, véase Difusión (desambiguación). Dibujo esquemático de los efectos de la difusión a través de una membrana celular. La difusión …   Wikipedia Español

  • Ecuación constitutiva — Saltar a navegación, búsqueda Una ecuación constitutiva es una relación entre las variables termodinámicas y/o mecánicas de un sistema físico: presión, volumen, tensión, deformación, temperatura, densidad, entropía, etc. Cada material o… …   Wikipedia Español

  • Ecuación de Arrhenius — La ecuación de Arrhenius es una expresión matemática que se utiliza para comprobar la dependencia de la constante de velocidad (o cinética) de una reacción química con respecto a la temperatura a la que se lleva a cabo esa reacción.[1] La… …   Wikipedia Español

  • Sistema de reacción-difusión — Los sistemas de reacción difusión son modelos matemáticos que describen cómo una o más sustancias distribuidas en el espacio cambian bajo la influencia de dos procesos: reacciones químicas locales en las que las sustancias se transforman las unas …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”