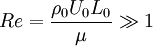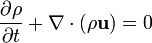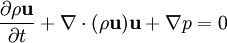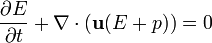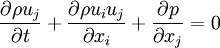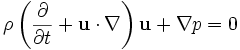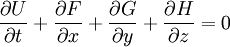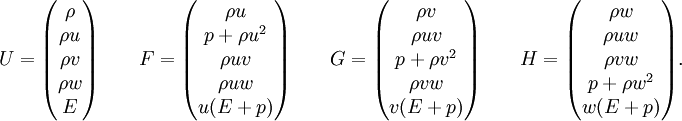Ecuaciones de Euler (fluidos)

Ecuaciones de Euler (fluidos)

Ecuaciones de Euler (fluidos)

Esta página trata sobre el flujo de fluidos compresibles. Mas ecuaciones de Euler en la Wikipedia en Ecuaciones de Euler.

En dinámica de fluidos, las ecuaciones de Euler son las que describen el movimiento de un fluido compresible no viscoso. Su expresión corresponde a las ecuaciones de Navier-Stokes cuando las componentes disipativas son despreciables frente a las convectivas, esto nos lleva a las siguientes condiciones que se pueden deducir a través del análisis de magnitudes de las Navier-Stokes:

Re=\frac{\rho_{0}U_{0}L_{0}}{\mu}\gg 1

Aunque habitualmente se expresan en la forma mostrada en este artículo dado que de este modo se enfatiza el hecho de que representan directamente la conservación de masa, momento y energía. Estas ecuaciones se llaman así en honor de Leonhard Euler quien las dedujo directamente de las leyes de Newton. Este artículo contempla las connotaciones aplicables a la mecánica clásica; para fluidos compresibles con velocidades próximas a la velocidad de la luz se debe consultar el artículo Ecuaciones relativistas de Euler.

Expresión matemática

Aunque formalmente las ecuaciones de Euler se reducen a flujo irrotacional en el límite de desaparición del número de Mach (es decir para números de Mach muy pequeños), esto no es útil en la práctica, debido esencialmente a que la aproximación de incompresibilidad no resta exactitud a los cálculos. La expresión diferencial de estas ecuaciones es la siguiente:

{\partial\rho\over\partial t}+ \nabla\cdot(\rho\bold u)=0
{\partial\rho{\bold u}\over\partial t}+ \nabla\cdot(\rho \bold u)\bold u+\nabla p=0
{\partial E\over\partial t}+ \nabla\cdot(\bold u(E+p))=0

donde E = ρe + ρ(u2 + v2 + w2) / 2 es la energía total por unidad de volumen (e es la energía interna por unidad de masa para el fluido), p es la presión, u la velocidad del fluido y ρ la densidad del fluido. La segunda ecuación incluye la divergencia de un tensor diádico y puede quedar más clara de acuerdo a la siguiente notación:

{\partial\rho u_j\over\partial t}+ {\partial\rho u_i u_j\over\partial x_i}+ {\partial p\over\partial x_j} =0

Nótese que las ecuaciones anteriores están expresadas en forma de conservación o equilibrio, dado que con esta forma se enfatiza su origen físico (y es además en gran medida la más conveniente para la simulación computacional de la dinámica de fluidos). El componente del momento de las ecuaciones de Euler se expresa del siguiente modo:

\rho\left( \frac{\partial}{\partial t}+{\bold u}\cdot\nabla \right){\bold u}+\nabla p=0

aunque esta forma oculta la conexión directa existente entre las ecuaciones de Euler y la segunda ley de Newton (en particular, no es claramente intuitivo por qué esta ecuación es correcta y 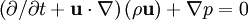\left(\partial/{\partial t}+{\bold u}\cdot\nabla\right)(\rho{\bold u})+\nabla p=0 no lo es). En formato vectorial las ecuaciones de Euler quedan expresadas del siguiente modo:

\frac{\partial U}{\partial t}+ \frac{\partial F}{\partial x}+ \frac{\partial G}{\partial y}+ \frac{\partial H}{\partial z}=0

donde

U=\begin{pmatrix}\rho \\ \rho u \\ \rho v \\ \rho w \\E\end{pmatrix}\qquad F=\begin{pmatrix}\rho u\\p+\rho u^2\\ \rho uv \\ \rho uw\\u(E+p)\end{pmatrix}\qquad G=\begin{pmatrix}\rho v\\ \rho uv \\p+\rho v^2\\ \rho vw \\v(E+p)\end{pmatrix}\qquad H=\begin{pmatrix}\rho w\\ \rho uw \\ \rho vw \\p+\rho w^2\\w(E+p)\end{pmatrix}.\qquad

Esta forma deja más claro que F,G,H son caudales.

Las ecuaciones anteriores representan por tanto la conservación de la masa, los tres componentes del momento y la energía. Hay por tanto cinco ecuaciones y seis incógnitas (ρ,u,v,w,E,p). Para cerrar el sistema se necesita una ecuación de estado; la ecuación de estado más comúnmente utilizada es la ley de los gases ideales ( p.e. p = ρ(γ − 1)e ).

Una característica muy importante de las Ecuaciones de Euler es que debido a que proceden de una reducción de las Ecuaciones de Navier-Stokes despreciando los términos provenientes de los términos disipativos como hemos dicho al principio, estamos eliminando en las ecuaciones los terminos en derivadas parciales de mayor grado: 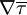\nabla \overline{\tau} en la Ecuación de la Cantidad de movimiento así como 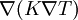\nabla (K \nabla T) y \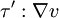tau ' : \nabla v de la Ecuación de la Energía, estas ecuaciones no podrán cumplir con todas las condiciones de contorno naturales. En particular no cumplen con la condición de no deslizamiento en las superficies de contacto con sólidos o la condición de continuidad de la temperatura, estas discontinuidades carecen de importancia para muchas aplicaciones pero no para otras lo que conlleva a tratar en esas discontinuidades con otras ecuaciones que finalmente conllevarían a temas muy profusos dentro de esta disciplina como es la Teoría de la Capa Límite. Por último hay que decir que en flujos supersónicos se producen otras discontinuidades en estas ecuaciones como son las Ondas de Choque o las Ondas de Mach.

Nótese la desigual forma para la ecuación de la energía; ver la ecuación de Rankine-Hugoniot. Los términos adicionales que contienen la expresión p (presión) pueden ser interpretados como el trabajo mecánico realizado por el fluido en un elemento de fluido por los elementos fluidos próximos que se mueven alrededor. Estos términos suman cero en un fluido incompresible.

La más conocida ecuación de Bernoulli puede ser obtenida integrando la ecuación de Euler a través de una línea de corriente (líneas a las que la velocidad del fluido es tangente en cada punto) asumiendo que la densidad es constante y con una ecuación de estado adecuada.

Véase también

Obtenido de "Ecuaciones de Euler (fluidos)"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Ecuaciones de Euler — Saltar a navegación, búsqueda En diversas áreas de la mecánica y las matemáticas existen diversas ecuaciones de Euler: En mecánica de fluidos tenemos las Ecuaciones de Euler (fluidos) para fluidos compresibles. En Mecánica del sólido rígido… …   Wikipedia Español

  • Ecuaciones de Euler — Esta página trata sobre el flujo de fluidos compresibles. Otras páginas relacionadas con los trabajos de Euler son fórmula de Euler e Identidad de Euler. En dinámica de fluidos, las ecuaciones de Euler son las que gobiernan el movimiento de un… …   Enciclopedia Universal

  • Ecuaciones de Navier-Stokes — Saltar a navegación, búsqueda Las ecuaciones de Navier Stokes reciben su nombre de Claude Louis Navier y George Gabriel Stokes. Se trata de un conjunto de ecuaciones en derivadas parciales no lineales que describen el movimiento de un fluido.… …   Wikipedia Español

  • Mecánica de fluidos — La mecánica de fluidos es la rama de la mecánica de medios continuos (que a su vez es una rama de la física) que estudia el movimiento de los fluidos (gases y líquidos) así como las fuerzas que los provocan.[1] La característica fundamental que… …   Wikipedia Español

  • Helicidad (mecánica de fluidos) — Para otros usos de este término, véase helicidad. En mecánica de fluidos, la helicidad es una magnitud física asociada al flujo que mide en cada punto del mismo la proyección de la vorticidad sobre la velocidad, dado que la combinación de un giro …   Wikipedia Español

  • Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… …   Wikipedia Español

  • Ecuación de continuidad — Saltar a navegación, búsqueda En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial. Contenido 1 Teoría Electromagnética 2 Mecánica de fluidos …   Wikipedia Español

  • Lagrangiano — En física, un lagrangiano es una función matemática a partir de la cual se pueden obtener la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico. De hecho, en física moderna el lagrangiano se… …   Wikipedia Español

  • Física — Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes. Sir …   Wikipedia Español

  • Teoría de campos — En física, la teoría de campos describe el conjunto de principios y técnicas matemáticas que permiten estudiar la dinámica y distribución espacial de los campos físicos. Así por ejemplo la teoría de campos permite describir específicamente como… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”