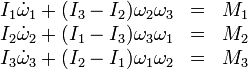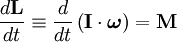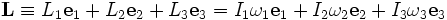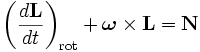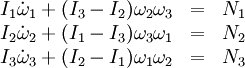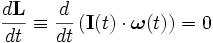Ecuaciones de Euler (sólidos)

Ecuaciones de Euler (sólidos)

Ecuaciones de Euler (sólidos)

En mecánica, las ecuaciones de Euler describen el movimiento de un sólido rígido en rotación en un sistema de referencia solidario con el sólido. Matemáticamente tienen la forma:

\begin{matrix} I_1\dot{\omega}_{1}+(I_3-I_2)\omega_2\omega_3 &=& M_{1}\\ I_2\dot{\omega}_{2}+(I_1-I_3)\omega_3\omega_1 &=& M_{2}\\ I_3\dot{\omega}_{3}+(I_2-I_1)\omega_1\omega_2 &=& M_{3} \end{matrix}


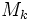donde M_{k} \, son las componentes vectoriales del momento o momento dinámico total aplicado, 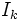I_{k} \, son los momentos principales de inercia y ωk son las componentes del vector velocidad angular 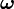\boldsymbol\omega según los ejes principales de inercia.

Contenido

Motivación y derivación

En un sistema de referencia inercial la derivada del momento angular es igual al momento dinámico o momento de fuerzas aplicado:

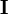\frac{d\mathbf{L}}{dt} \equiv \frac{d}{dt} \left( \mathbf{I} \cdot \boldsymbol\omega \right) = \mathbf{M}

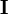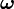Donde \mathbf{I} es el tensor de momentos de inercia. Sin embargo, aunque la ecuación anterior es universalmente válida, no resulta útil en la práctica para calcular el movimiento puesto que generalmente, tanto \mathbf{I} como \boldsymbol\omega varían con el tiempo.

Sin embargo, el problema anterior se resuelve si consideramos un sistema de referencia no-inercial solidario con el sólido rígido en rotación, porque respecto a este sistema de referencia el tensor de [momentos de] inercia 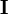\mathbf{I} es constante y sólo la velocidad angular 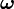\boldsymbol\omega varía con el tiempo. De hecho de todos los posibles sistemas de este tipo tomaremos por simplicidad y conveniencia matemática uno cuyos ejes coincidan con las direcciones principales de inercia (que permiten forman un triedro rectángulo). En estas condiciones el vector momento angular puede escribirse como:

\mathbf{L} \equiv L_{1}\mathbf{e}_{1} + L_{2}\mathbf{e}_{2} + L_{3}\mathbf{e}_{3} = I_{1}\omega_{1}\mathbf{e}_{1} + I_{2}\omega_{2}\mathbf{e}_{2} + I_{3}\omega_{3}\mathbf{e}_{3}

Donde Ik son los momentos de inercia principales, 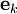\mathbf{e}_{k} son los vectores unitarios en la dirección de los ejes principales de inercia y ωk son las componentes de la velocidad angular expresadas en la base formada por los vectores unitarios anteriores. En un sistema no-inercial giratorio, la derivada temporal debe ser reemplazada por otra expresión que de cuenta también de las fuerzas ficticias asociadas a la no-inercialidad del sistema:

\left(\frac{d\mathbf{L}}{dt}\right)_\mathrm{rot}+ \boldsymbol\omega\times\mathbf{L}=\mathbf{N}

Donde el subíndice rot indica que una magnitud se computa en el sistema no-inercial rotatorio. Substituyendo 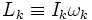L_{k} \equiv I_{k}\omega_{k}, tomando el producto vectorial y usando el hecho de que los momentos principales de inercia no varían con el tiempo, llegamos a las ecuaciones de Euler:

\begin{matrix} I_1\dot{\omega}_{1}+(I_3-I_2)\omega_2\omega_3 &=& N_{1}\\ I_2\dot{\omega}_{2}+(I_1-I_3)\omega_3\omega_1 &=& N_{2}\\ I_3\dot{\omega}_{3}+(I_2-I_1)\omega_1\omega_2 &=& N_{3} \end{matrix}

Rotación libre en el espacio

Cuando el momento dinámico es nulo tenemos una solución de movimiento libre. Puesto que en general la velocidad angular no coincide con ninguno de los ejes principales de inercia lo cual se traduce en un movimiento de precesión carecterizado porque el eje de rotación se mueve alrededor de la recta que coincide con la dirección del momento angular y otro de nutación caracterizado porque el eje de rotación oscila variando su ángulo con la dirección del momento angular.

Se puede ver porqué sucede a partir de la ecuaión de movimiento expresada en un sistema inercial cuando el momento es cero:

\frac{d\mathbf{L}}{dt} \equiv \frac{d}{dt} \left( \mathbf{I}(t) \cdot \boldsymbol\omega (t) \right) = 0

Puesto que para un sólido giratorio 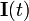\mathbf{I}(t) varía con el tiempo, la única manera de que 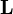\mathbf{L} sea constante es que 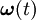\boldsymbol\omega (t) también varíe con el tiempo.

Véase también


Referencias

  • Landau LD and Lifshitz EM (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover).
  • Goldstein H. (1980) Classical Mechanics, 2nd. ed., Addison-Wesley. ISBN 0-201-02918-9
  • Symon KR. (1971) Mechanics, 3rd. ed., Addison-Wesley. ISBN 0-201-07392-7
Obtenido de "Ecuaciones de Euler (s%C3%B3lidos)"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Ecuaciones de Euler — Saltar a navegación, búsqueda En diversas áreas de la mecánica y las matemáticas existen diversas ecuaciones de Euler: En mecánica de fluidos tenemos las Ecuaciones de Euler (fluidos) para fluidos compresibles. En Mecánica del sólido rígido… …   Wikipedia Español

  • Ecuaciones de Euler (fluidos) — Saltar a navegación, búsqueda Esta página trata sobre el flujo de fluidos compresibles. Mas ecuaciones de Euler en la Wikipedia en Ecuaciones de Euler. En dinámica de fluidos, las ecuaciones de Euler son las que describen el movimiento de un… …   Wikipedia Español

  • Leonhard Euler — Retrato de Leonhard Euler, pintado por Johann Georg Bruck …   Wikipedia Español

  • Mecánica del sólido rígido — Movimiento complejo de un sólido rígido, que presenta precesión alrededor de la dirección del momento angular además rotación según su eje de simetría La mecánica de un sólido rígido es aquella que estudia el movimiento y equilibrio de sólidos… …   Wikipedia Español

  • Rotor rígido — Saltar a navegación, búsqueda El rotor rígido es un modelo que se utiliza para explicar el movimiento de los sistemas que rotan. Un rotor rígido es un objeto rígido tridimensional, por ejemplo un trompo o peonza. Para orientar dicho objeto en el… …   Wikipedia Español

  • Lagrangiano — En física, un lagrangiano es una función matemática a partir de la cual se pueden obtener la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico. De hecho, en física moderna el lagrangiano se… …   Wikipedia Español

  • Física — Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes. Sir …   Wikipedia Español

  • Ecuación de estado — Saltar a navegación, búsqueda En física y química, una ecuación de estado es una ecuación constitutiva para sistemas hidrostáticos que describe el estado de agregación de la materia como una relación funcional entre la temperatura, la presión, el …   Wikipedia Español

  • Principio de d'Alembert — Saltar a navegación, búsqueda Retrato de Jean d Alembert. El principio de d Alembert, enunciado por Jean d Alembert en su obra maestra Tratado de dinámica de 1743, establece que la suma de las fuerzas externas que actúan sobre un cuerpo y las… …   Wikipedia Español

  • Lenguaje formalizado — El lenguaje formalizado es un lenguaje sometido a unas «reglas fijas de formación de expresiones y significados». Es una de las características esenciales del lenguaje científico. Incluso hay autores que llegan a opinar que la ciencia en sí misma …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”