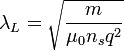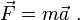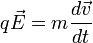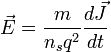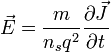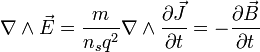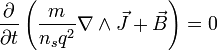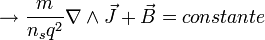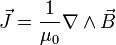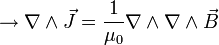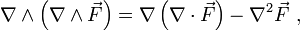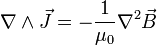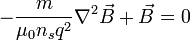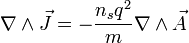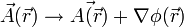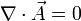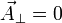Efecto Meissner

Efecto Meissner

Efecto Meissner

Imán levitando sobre un material superconductor. Para experimentar los efectos de la superconductividad es necesario enfriar la muestra a muy bajas temperaturas.
Expulsión del campo magnético por debajo de la temperatura crítica.

El efecto Meissner, también denominado efecto Meissner-Ochsenfeld, consiste en la desaparición total del flujo del campo magnético en el interior de un material superconductor por debajo de su temperatura crítica. Fue descubierto por Walter Meissner y Robert Ochsenfeld en 1933 midiendo la distribución de flujo en el exterior de muestras de plomo y estaño enfriados por debajo de su temperatura crítica en presencia de un campo magnético.

Meissner y Ochsenfeld encontraron que el campo magnético se anula completamente en el interior del material superconductor y que las líneas de campo magnético son expulsadas del interior del material, por lo que este se comporta como un material diamagnético perfecto. El efecto Meissner es una de las propriedades que definen la superconductividad y su descubrimiento sirvió para deducir que la aparición de la superconductividad es una transición de fase a un estado diferente.

La expulsión del campo magnético del material superconductor posibilita la formación de efectos curiosos, como la levitación de un imán sobre un material superconductor a baja temperatura que se muestra en la figura.


Contenido

La ecuación de London

La primera teoría fenomenológica que explica el efecto Meissner se basa en la ecuación de London,

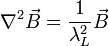
(1) \nabla^2\vec{B}=\frac{1}{\lambda^2_L}\vec{B}

donde λL depende de la cantidad ns de electrones (por unidad de volumen, es decir, densidad) que se encuentran en estado superconductor:

\lambda_L=\sqrt{\frac{m}{\mu_0 n_sq^2}}

La ecuación, desarrollada por los hermanos Fritz y Heinz London en 1935,[1] explica la forma que ha de tener un campo magnético para que se cumplan las condiciones fundamentales que se dan en el efecto Meissner, que son:

  1. que el campo magnético sea nulo en el interior del superconductor,
  2. que las corrientes eléctricas estén limitadas a la superficie del superconductor, en una capa de un espesor del orden de lo que se conoce como la longitud de penetración λL, siendo nulas en el interior.

Los hermanos London desarrollaron su teoría pensando que los portadores de carga eran electrones, lo cual se vio que era erróneo varias décadas después. Sin embargo, a pesar de este desacierto inicial, los resultados experimentales no se vieron muy afectados debido a que la longitud de penetración es esencialmente la misma en ambos casos:

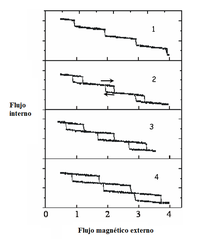Cuantización del campo magnético en un anillo superconductor.[2]
magnitud idea inicial de los hermanos London idea posterior con pares de Cooper
carga q -e (carga de un electrón) -2e
masa m me (masa de un electrón) 2me
densidad de partículas en estado superconductor ns ns/2
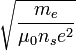
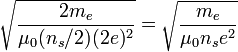
longitud de penetración λL \sqrt{\frac{m_e}{\mu_0 n_se^2}} \sqrt{\frac{2m_e}{\mu_0 (n_s/2)(2e)^2}} = \sqrt{\frac{m_e}{\mu_0 n_se^2}}

El primero en darse cuenta del error fue Lars Onsager en 1953 investigando la cuantización del flujo magnético que pasa por un anillo superconductor: el valor mínimo del flujo le salía exactamente la mitad de lo que debía ser, lo cual está acorde con una carga 2e. Basándose en esta idea Cooper expondría la idea de que los portadores de carga no son en realidad electrones, sino parejas de electrones[3] (conocidas como pares de Cooper), como se explicó con todo detalle en la teoría BCS más tarde.

La ecuación de Pippard

La ecuacuón de London (1) tiene diversas limitaciones. La principal de ellas es que no respeta el principio fundamental de la física según el cual dos sucesos lo suficientemente alejados uno de otro no pueden interferir entre sí. Dicho de otra forma, se trata de una teoría no local. Esto se debe a que los dos electrones que forman el par de Cooper están relativamente alejados uno de otro. No obstante, en su momento los hermanos London no podían saber esto, ya que ni siquiera sabían que se trataba de dos electrones juntos en lugar de uno.

Para resolver esto Brian Pippard presentó 1953 la ecuación de Pippard, que es más general que la de los hermanos London, y fue corroborada poco más tarde por la teoría BCS.

El efecto Meissner cuando nos acercamos a la temperatura crítica

Debido a la dependencia de la longitud de penetración con la densidad de electrones en el estado superconductor, es fácil ver que cuanto más se acerque la temperatura de la muestra a la temperatura crítica, menos electrones habrá en estado superconductor y por lo tanto el campo magnético penetrará cada vez más en el superconductor. Cuando el superconductor alcanza la temperatura crítica la longitud de penetración tiende a infinito, lo que significa que el campo magnético puede penetrar en la muestra sin oposición alguna, es decir, el efecto Meissner desaparece.

Históricamente fue difícil comprender por qué la longitud de penetración aumentaba con la temperatura, ya que no se supo hasta más tarde que los electrones en estado superconductor (es decir, aquellos que están de dos en dos formando pares de Cooper) conviven con los electrones en estado normal (es decir, desapareados), y que la densidad de electrones en un estado u otro depende de la temperatura.

Valores típicos de la longitud de penetración

Teniendo en cuenta la definición dada más arriba, tomando los valores correspondientes a las constantes y dando a la densidad de electrones en estado superconductor ns un valor típico de unos 1023 electrones por cm3 (que será menor a medida que la temperatura se acerque a la crítica) obtenemos una longitud de penetración λL ~ 1700 Å, lo que corresponde a una penetración entre los centenares y los millares de capas atómicas, lo cual corresponde bastante bien con los valores experimentales.

Teoría

Deducción de la ecuación de London

La ecuación (1) se puede deducir mediante un tratamiento completamente clásico, y, aparte de las dos condiciones planteadas, nos bastan las ecuaciones de Maxwell y la segunda ley de Newton

\vec{F}=m\vec{a} \ .


La segunda ley de Newton se puede expresar en este caso como

q\vec{E} = m\frac{d\vec{v}}{dt}

Tomando la densidad de corriente 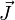\vec{J} en lugar de la velocidad y pasando la carga q al otro lado obtenemos:

\vec{E} = \frac{m}{n_sq^2}\frac{d\vec{J}}{dt}

si bien no es más que la segunda ley de Newton expresada en términos de la densidad de corriente y campo eléctrico.

Si consideramos que la velocidad de los electrones es pequeña, podemos tomar derivadas parciales en lugar de derivadas totales, y obtenemos la que en algunos textos se conoce como la primera ecuación de London (siendo la segunda la ecuación de London propiamente dicha),

\vec{E} = \frac{m}{n_sq^2}\frac{\partial\vec{J}}{\partial t}

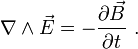
Si ahora hacemos el rotacional a ambos lados de la ecuación, entra en juego las ecuaciones de Maxwell, en concreto la ley de Faraday: \nabla\wedge\vec{E} = - \frac{\partial\vec{B}}{\partial t} \ .

\nabla\wedge\vec{E} = \frac{m}{n_sq^2}\nabla\wedge\frac{\partial\vec{J}}{\partial t} = - \frac{\partial\vec{B}}{\partial t}

lo cual podemos rexpresar como

\frac{\partial}{\partial t} \left ( \frac{m}{n_sq^2}\nabla\wedge\vec{J}+\vec{B} \right ) = 0
\rightarrow \frac{m}{n_sq^2}\nabla\wedge\vec{J}+\vec{B} = constante

Pero si tenemos en cuenta la primera condición (que el campo magnético y la densidad de corriente sean nulas en el interior del superconductor) vemos que esta constante ha de ser igual a cero y nos queda

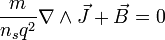
(2) \frac{m}{n_sq^2}\nabla\wedge\vec{J}+\vec{B} = 0

Ahora bien, lo que nos interesa es tener todo en función del campo magnético, así que tenemos que deshacernos de la densidad de corriente. Esto se puede hacer empleando otra ecuación de Maxwell, la ley de Ampère

\vec{J}=\frac{1}{\mu_0}\nabla\wedge\vec{B}
\rightarrow\nabla\wedge\vec{J}=\frac{1}{\mu_0}\nabla\wedge\nabla\wedge\vec{B}

para deshacernos del rotacional de un rotacional, que es más bien incómodo, podemos aplicar la conocida indentidad según la cual para cualquier campo 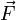\vec{F} tenemos que

\nabla\wedge\left( \nabla\wedge\vec{F} \right) = \nabla \left( \nabla\cdot\vec{F}\right) - \nabla^2\vec{F} \ ,

Haciendo un último uso de las ecuaciones de Maxwell consideramos que para un campo magnético 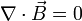\nabla\cdot\vec{B}=0, por lo que el primer término de la parte de la derecha se anula y ya podemos deshacernos del rotacional de la densidad de corriente:

\nabla\wedge\vec{J} = -\frac{1}{\mu_0}\nabla^2\vec{B}

Que no es más que la ley de Ampère expresada de otra manera. Si ahora lo reemplazamos en la ecuación con la que estábamos trabajando, nos queda que

-\frac{m}{\mu_0 n_sq^2}\nabla^2\vec{B} + \vec{B} = 0

con lo que ya sólo tenemos que agrupar las constantes en 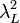\lambda^2_L y pasar uno de los términos al otro lado del igual para obtener la ecuación de London (1), que era nuestro objetivo.

Ecuación de London respecto al potencial vector

Es posible expresar la ecuación de London (1) también como:

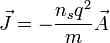
(3) \vec{J}=-\frac{n_sq^2}{m}\vec{A}

Donde 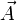\vec{A} es el potencial vector. Para llegar a esta expresión basta con tomar del desarrollo anterior la ecuación intermedia (2); teniendo en cuenta que, por definición

\vec{A}=\nabla\wedge\vec{B} ,

llegamos a

\nabla\wedge\vec{J}=-\frac{n_sq^2}{m}\nabla\wedge\vec{A}

y quitando los rotacionales tendremos la ecuación buscada.

Nota: no hay que olvidar que no se pueden quitar los rotacionales a la ligera, ya que nos aparece que, con el mismo resultado, podemos añadir al potencial vector una función 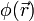\phi(\vec{r}) tal que

\vec{A}(\vec{r})\rightarrow\vec{A(\vec{r})}+\nabla\phi(\vec{r})

sin embargo, en el problema que estamos tratando podemos aplicar el gauge de London,

\nabla\cdot\vec{A}=0
\vec{A}_\perp=0

con lo que, si el superconductor es un sólido simplemente conexo, tendremos que 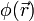\phi(\vec{r}) es en realidad constante y no influye en el problema.

Referencias

  1. ↑ F. London and H. London (marzo de 1935). «The Electromagnetic Equations of the Supraconductor» Proceedings of the Royal Society A. Vol. 149. n.º 866. pp. 71-88. DOI 10.1098/rspa.1935.0048.
  2. ↑ MG Castellano y otros (2003). «Tracing the characteristics of a flux qubit with a hysteretic dc-superconducting quantum interference device comparator» Journal of Applied Physics. Vol. 94. pp. 7935. DOI 10.1063/1.1628382.
  3. ↑ LN Cooper (noviembre de 1956). «Bound Electron Pairs in a Degenerate Fermi Gas» Physical Review. Vol. 104. n.º 4. pp. 1189 - 1190. DOI 10.1103/PhysRev.104.1189.

Enlaces externos

Efecto Meissner en YouTube

Obtenido de "Efecto Meissner"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Efecto Meissner — El efecto Meissner, también denominado efecto Meissner Ochsenfeld, consiste en la desaparición total de campo magnético en el interior de un material superconductor por debajo de su temperatura crítica. Fue descubierto por Walter Meissner y… …   Enciclopedia Universal

  • Efecto — Saltar a navegación, búsqueda Para la técnica deportiva, véase chanfle, massé y efecto Magnus. La palabra efecto (del latín effectus) tiene una gran cantidad de significados, ligados muchos de ellos a la experimentación científica, porque su… …   Wikipedia Español

  • Walter Meissner — Walter Meissner. Fritz Walter Meißner (Berlín, 16 de diciembre de 1882 Múnich, 16 de noviembre de 1974) fue un físico alemán. Meissner estudió en Berlín construcción de máquinas y física siendo alumno de Max Planck. Tras estos estudios comenzó a… …   Wikipedia Español

  • Walter Meissner — Walter Meißner, físico alemán (16 de diciembre de 1882, Berlín 16 de noviembre de 1974, Munich). Físico alemán. Meissner estudió en Berlín construcción de máquinas y física siendo alumno de Max Planck. Tras estos estudios comenzó a trabajar en el …   Enciclopedia Universal

  • Superconductividad — Problemas no resueltos de la física: Superconductores de alta temperatura: ¿Por qué ciertos materiales muestran superconductividad a temperaturas mucho mayores de 50 K? …   Wikipedia Español

  • Levitación — Un imán cúbico levitando sobre un material superconductor. Se denomina levitación el efecto por el que un cuerpo u objeto se halla en suspensión estable en el aire, sin mediar de otro objeto físico en contacto con el primero que sustente al que… …   Wikipedia Español

  • Campo magnético crítico — Saltar a navegación, búsqueda El campo magnético crítico, Bc, (o su equivalente intensidad de campo magnética crítica, Hc) es el valor del campo magnético a partir del cual un superconductor que está a una temperatura fija inferior a su… …   Wikipedia Español

  • Superconductor de tipo I — Comportamiento típico de un superconductor de tipo I en presencia de un campo magnético. Los superconductores de tipo I son superconductores que en presencia de un campo magnético establecen corrientes superficiales que impiden que dicho campo… …   Wikipedia Español

  • Superconductor de tipo II — Diferencia entre las reacciones a un campo magnético externo de un superconductor de tipo I (en rojo) y un superconductor de tipo II (en azul). Para contrarrestar el campo externo, el superconductor adquiere una magnetización que cae bruscamente… …   Wikipedia Español

  • Teoría BCS — Placa en la Universidad de Illinois, donde se conmemora el Premio Nobel recibido por John Bardeen gracias al desarrollo de la teoría BCS. La Teoría BCS (que recibe su nombre de las iniciales de quienes la idearon: John Bardeen, Leon Cooper, y… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”