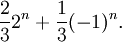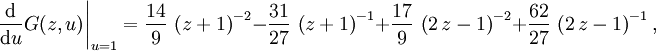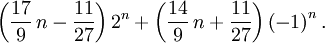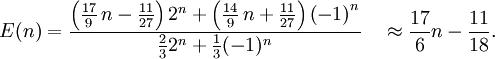- Ejemplos de funciones generadoras
-
Ejemplos de funciones generadoras
Los siguientes ejemplos de funciones generadoras se presentan siguiendo el espíritu de George Pólya, que abogaba por el aprendizaje de las matemáticas haciendo y repasando tantos ejemplos y pruebas como fuese posible. El objetivo de este artículo es presentar trucos comunes del oficio en su contexto, de manera que el lector pueda incorporarlos a sus conocimientos.
Contenido
Ejemplo resuelto A: básico
Se pueden crear nuevas funciones generadoras expandiendo otras funciones generadoras más simples. Por ejemplo, comenzando con:
y sustituyendo x por 2x, obtenemos:
Ejemplo resuelto B: números de Fibonacci
Consideremos el problema de hallar una fórmula cerrada para los números de Fibonacci Fn definidos por F0 = 0, F1 = 1, y Fn = Fn−1 + Fn−2 para n ≥ 2. Formamos la función generadora ordinaria
para esta sucesión. La función generadora para la sucesión (Fn−1) es xf y la de (Fn−2) es x2f. A partir de la relación de recurrencia, vemos, por lo tanto, que la serie de potencias xf + x2f concuerda con f excepto en los dos primeros coeficientes:
Teniendo en cuenta éstos, hallamos que
(Este es el paso crucial; las relaciones recurrentes casi siempre pueden traducirse a ecuaciones para las funciones generadoras.) Resolviendo esta ecuación para f, obtenemos
El denominador puede factorizarse utilizando la proporción áurea φ1 = (1 + √5)/2 y φ2 = (1 − √5)/2, y la técnica de descomposición en fracciones parciales nos da:
Estas dos series formales de potencias se conocen expresamente porque son series geométricas; comparando coeficientes, hallamos la fórmula explícita
Ejemplo resuelto C: aristas en un grafo no orientado
El foco de este ejemplo es el uso de las funciones generadoras en muchas variables para alcanzar la meta de clasificar los elementos m de un conjunto E de acuerdo con muchos parámetros
 a través de la correspondencia
a través de la correspondencia  . Aquí las variables de la función generadora son
. Aquí las variables de la función generadora son 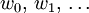 y la función generadora f es
y la función generadora f esde modo que el número c de elementos de E que corresponden a la tupla de parámetros
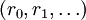 es dado por
es dado pordonde hemos usado el operador de extracción de coeficientes para la serie formal de potencias.
El ejemplo que estudiaremos concierne a un grafo no dirigido G = (V,E) cuyos vértices V corresponden a palabras de longitud t a partir de un alfabeto Σ que contiene exactamente l letras, es decir:
En lo que sigue, utilizaremos los números de 0 a l − 1 en lugar de las letras, para mantener una notación sencilla.
Además, nos dan un conjunto de funciones
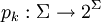 que determinan cuál de los vértices posibles
que determinan cuál de los vértices posibles 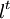 aparecen en el grafo, y cuáles son las aristas. De modo más preciso, pk(λ) especifica un conjunto de posibles sustitutos para λ, si se presenta en una posición k. En ese caso, λ puede cambiarse por cualquier letra que se presente en pk(λ), dando una palabra adyacente, esto es, un vértice. Las aristas existen entre las palabras adyacentes, pero sólo si difieren exactamente en una posición. Hablando intuitivamente, los pk ofrecen los vecinos de una letra particular que se presenta en una posición k, y los vecinos de una palabra son las palabras que pueden obtenerse seleccionando una posición y reemplazando la letra λ en esa posición por uno de sus vecinos, es decir, un elemento de pk(λ). Queda garantizado que los pk son tales que la adyacencia siempre funciona en ambos sentidos, esto es, si
aparecen en el grafo, y cuáles son las aristas. De modo más preciso, pk(λ) especifica un conjunto de posibles sustitutos para λ, si se presenta en una posición k. En ese caso, λ puede cambiarse por cualquier letra que se presente en pk(λ), dando una palabra adyacente, esto es, un vértice. Las aristas existen entre las palabras adyacentes, pero sólo si difieren exactamente en una posición. Hablando intuitivamente, los pk ofrecen los vecinos de una letra particular que se presenta en una posición k, y los vecinos de una palabra son las palabras que pueden obtenerse seleccionando una posición y reemplazando la letra λ en esa posición por uno de sus vecinos, es decir, un elemento de pk(λ). Queda garantizado que los pk son tales que la adyacencia siempre funciona en ambos sentidos, esto es, si 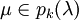 , entonces
, entonces 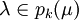 . Las palabras que contienen letras en posiciones en las que no tienen vecinos, es decir, en las que | pk(λ) | = 0, se omiten en el conjunto de vértices. La cuestión que tratamos de responder es: ¿cuántas aristas contiene este grafo?
. Las palabras que contienen letras en posiciones en las que no tienen vecinos, es decir, en las que | pk(λ) | = 0, se omiten en el conjunto de vértices. La cuestión que tratamos de responder es: ¿cuántas aristas contiene este grafo?El conjunto cuyos elementos tratamos de enumerar y clasificar aquí es el conjunto de vértices V, y tenemos que clasificar los vértices m de acuerdo con el número de letras que tienen
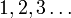 vecinos, de modo que
vecinos, de modo quesiendo r1(m) el número de letras que tienen un vecino en su posición, r2(m) el número de letras que tienen dos vecinos en su posición, etc., porque entonces el número de aristas que se originan en m es dado por
Esto se debe a que
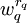 indica la presencia derq letras que tienen q vecinos en m, que aportan
indica la presencia derq letras que tienen q vecinos en m, que aportan  aristas, pero
aristas, peroEste proceso contará las aristas dos veces (una vez en cada extremo), dando finalmente la fórmula para el número T de aristas
Falta por hallar
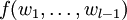 . Con esto en mente, introducimos las cantidades vk(q), el número de letras de una posición k que tienen q vecinos, esto es,
. Con esto en mente, introducimos las cantidades vk(q), el número de letras de una posición k que tienen q vecinos, esto es,También nos hará falta Lk, el número de letras que de hecho se presentan en la posición k, es decir,
- Lk = l − vk(0).
(Recuérdese que todas las letras que no tienen vecinos no contribuyen al conjunto de vértices posibles.)
Entonces, la función generadora f es dada por
Calcular la respuesta
Es así que T se puede calcular explícitamente, dando una fórmula sencilla y útil. Este cálculo se basa en la observación de que
equivale a
que se simplifica como
y resulta
Un ejemplo sencillo
Tomemos Σ = {0,1,2}, de modo que l = 3, y consideremos las palabras (vértices) que consisten en dos letras, es decir, t = 2. El conjunto de funciones vecinas pk es dado por
La función generadora se convierte en
Extrayendo la diferenciación, hallamos la siguiente expresión para T:
o bien
así que podemos esperar siete aristas.
De hecho, estas aristas son
El resultado encaja con lo que obtenemos sustituyendo en la fórmula. Tenemos
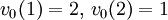 y
y 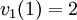 , y L0 = 3 y L1 = 2, lo que da
, y L0 = 3 y L1 = 2, lo que daCaso especial
Hay un caso especial importante que ofrece una fórmula más sencilla para T. Este es el caso de cuando no hay letras «inertes», es decir, cuando todas las letras tienen vecinos o bien vk(0) = 0 en todas las posiciones, lo que implica que Lk = l para todo k. La fórmula simplificada se convierte en
Supóngase, por ejemplo, que todas las letras son adyacentes a las que difieren en una unidad de su valor numérico, independiente de su posición. De ahí que haya dos letras que tienen un vecino (a saber, 0 y l − 1), y las demás letras tienen dos vecinos. De la sustitución resulta entonces
Este ejemplo se ha tomado de Les-Mathematiques.net. Algunas variaciones de este problema, incluyendo una considerable cantidad de material adicional, pueden encontrarse en los «Enlaces externos».
Ejemplo resuelto D: funciones generadoras en dos variables y sumas de los dígitos
Las funciones generadoras ordinarias no se limitan a representar sucesiones que dependen únicamente de un solo parámetro. Son posibles más parámetros, dos o más, como se ha visto en el ejemplo previo. También es posible mezclar tipos de funciones generadoras, por ejemplo funciones generadoras de probabilidad en dos variables, donde una función generadora ordinaria genera una exponencial. A menudo se denomina a estos tipos de funciones generadoras «super funciones generadoras». Aquí se muestra un ejemplo de cómo trabajar con funciones generadoras en dos variables.
Sea n un número natural y consideremos los enteros desde 0 a 102n − 1, donde esos enteros que tienen menos de 2n dígitos se completan con ceros a la izquierda, de forma que de todos ellos pueda considerarse que tienen 2n dígitos. Por ejemplo, para n = 3 el abanico va desde 000000 hasta 999999. Emplearemos funciones generadoras en dos variables para responder la siguiente cuestión: ¿cuál es la suma de los enteros en [0,102n − 1] cuyos primeros n dígitos suman el mismo valor que los últimos n dígitos, esto es, la suma de los dígitos de la primera mitad de los cuales es igual a la suma de los dígitos de la segunda mitad? A estos enteros los llamamos equilibrados. Por ejemplo, el entero 124511 sería parte de la suma con n = 3, ya que 1+2+4=7=5+1+1. El valor que aportaría es sencillamente 124511. Ciertamente es imposible calcular esta suma por enumeración directa para grandes n (tómese n = 20, por ejemplo).
Sea En la denotación de la suma deseada, e introdúzcase gn,k, que da el número de enteros n cifras de largo (completándolos con ceros como antes, para obtener 10n valores) cuyas cifras suman k, y sn,k, que es la suma de los enteros n cifras de largo cuyas cifras suman k. La observación clave aquí es darse cuenta de que
Para ver esto, establézcase k, la suma de los dígitos, y considérese el conjunto de enteros equilibrados de longitud 2n, la suma de los dígitos de la primera y la segunda mitad de los cuales es k. Este conjunto de enteros se crea emparejando cualquier entero de longitud n y suma de los dígitos k con cualquier otro, de modo que se presenta cualquier valor particular gn,k veces en la primera mitad (multiplicado por 10n), y gn,k veces en la segunda mitad. Añadiendo todos estos enteros, resulta sn,k. El número de sumandos que contribuyen a En es dado por
Ahora introducimos las dos siguientes funciones generadoras en dos variables:
(Se requiere que gn,k = 0 y sn,k = 0 para k > 9n, porque 9n es la suma de los dígitos máxima posible.) También se requieren dos funciones auxiliares para mantener la notación sencilla:
Ahora, por la definición de G(z,u), se sigue inmediatamente que
Esto se debe a que los términos de V(u)n representan el proceso de escoger un dígito decimal para la primera posición de la izquiera, uno para la segunda, y así sucesivamente. Los exponentes se añaden de forma que el término uk se presente cada vez que los dígitos suman k.
La siguiente observación clave es que para
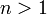 ,
,Esto quiere decir sencillamente que los enteros que contribuyen a
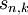 se pueden obtener a partir de los que contribuyen a
se pueden obtener a partir de los que contribuyen a  , donde r es un dígito decimal, moviendo los últimos una posición a la izquierda (multiplicación por diez) y añadiendo r (recuérdese que hay
, donde r es un dígito decimal, moviendo los últimos una posición a la izquierda (multiplicación por diez) y añadiendo r (recuérdese que hay 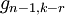 enteros que contribuyen a
enteros que contribuyen a  )
)Ahora nos disponemos a reconstituir S(z,u) sumando la recurrencia de arriba con
 . El término para
. El término para ![[z^1] S(z, u)\,](/pictures/eswiki/55/73c3fe67efe370607129da64085f1dc7.png) , esto es, n = 1, faltará en la suma de la izquierda, así que lo calculamos y lo añadimos. (En lo que sigue utilizaremos el operador de extracción de coeficientes para la serie de potencias formales.) Tenemos
, esto es, n = 1, faltará en la suma de la izquierda, así que lo calculamos y lo añadimos. (En lo que sigue utilizaremos el operador de extracción de coeficientes para la serie de potencias formales.) TenemosAñadiendo todo, hallamos que
de donde
o bien
lo cual es una simple función generadora racional.
Recordemos nuestra fórmula inicial, que podemos reescribir como
Ahora podemos calcular el En, ya que tenemos formas cerradas para G(z,u) y S(z,u). Esto nos da la siguiente tabla para n y En:
1 495 2 3349665 3 27625972374 4 240801497591985 5 2162288199783771180 . ... 17 1185633898500558643116053969483499881436610149944135688394603051650 18 11525195623906119101843912373578899988474804376093880898156087626421100 19 112203312767859412537217211281711779998877966872321405874627827887182882200 20 1093844474149520613133628019194480743399890615552585047938686637198080551925660.Fórmula explícita alternativa
Una fórmula explícita para En, que sin embargo no es tan receptiva al cálculo simbólico como la forma previa, se puede obtener extendiendo la serie geométrica en la descomposición en fracciones parciales de
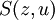 y empleando la simetría de
y empleando la simetría de ![[z^n] G(z, u)\,](/pictures/eswiki/102/fae9d456d9d30c54917d53b6a2218f8d.png) para observar que
para observar quelo cual nos da
Pero
de modo que
Recurrencia alternativa
El lector sagaz habrá observado que obtuvimos la recurrencia para sn,k añadiendo el dígito r a uno de los contribuyentes de
 . Por supuesto, es enteramente posible preañadir r a esos contribuyentes, lo que resulta en la recurrencia alternativa
. Por supuesto, es enteramente posible preañadir r a esos contribuyentes, lo que resulta en la recurrencia alternativaSumando como antes, hallamos
Resolver esto para S(z,u) produce, como esperábamos, la misma solución que antes:
Verificación
Cuando se trabaja con funciones generadoras, es importante verificar que producen valores razonables. Al poner variables de funciones generadoras ordinarias multivariables en una sola, obtenemos funciones generadoras de superclases de estructuras o cantidades combinatorias, ya que uno o más de los parámetros desaparecen. Por ejemplo,
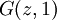 es la función generadora de la cuenta total de enteros no negativos de n dígitos, en la cual se usa el completado con ceros a la izquierda. De hecho, tenemos
es la función generadora de la cuenta total de enteros no negativos de n dígitos, en la cual se usa el completado con ceros a la izquierda. De hecho, tenemoslo cual es correcto. De modo similar.
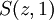 es la función generadora de la suma de todos los enteros no negativos de n dígitos, de nuevo completando por la izquierda con ceros. Tenemos
es la función generadora de la suma de todos los enteros no negativos de n dígitos, de nuevo completando por la izquierda con ceros. TenemosDe ahí
Este también es el valor correcto, ya que
Material adicional en relación con este ejemplo, así como una instantánea de cómo se desarrolló, puede encontrarse en los «Enlaces externos«.
Ejemplo resuelto E: pseudo números romanos
Considérese un sistema numérico creado empleando un subconjunto de las reglas y las letras de los números romanos. Específicamente tenermos las letras I, V y X con los valores 1, 5 y 10, cualquier sucesión de los cuales se considera un número cuyo valor es la suma de las cifras individuales. En otras palabras, tenemos un alfabeto
y consideramos los elementos de Σ * .
Cada letra tiene un peso que corresponde al número de barras que hacen falta para dibujar esa letra. Consideramos que I tiene peso uno y que X y V tienen ambas peso dos, al consistir en dos barras cruzadas la primera y en dos barras adyacentes con un punto base común la segunda. El peso de una palabra, es decir, número, es la suma de los pesos de los dígitos que la constituyen. Por ejemplo, el valor de XXVI es 26 y su peso es 2 + 2 + 2 + 1 = 7. Ahora formulamos la siguiente pregunta: ¿qué valor se puede esperar del valor de un número que tiene peson?
Empleamos la siguiente función generadora ordinaria para responder la pregunta:
donde el monomio znuk representa una palabra de n barras (peso n) que tiene un valor k. Sea vn = [zn]G(z,u). Por definición, tenemos
Sumando la recurrencia con n hallamos
lo que da la siguiente ecuación para G(z,u):
Resolviendo para G, obtenemos
El valor esperado E(n) de una palabra de peso no es dado por la fórmula
donde el numerador es la suma de los valores de todas las palabras que tienen peso n, y el denominador es el número de esas palabras.
Comencemos con el denominador. Tenemos
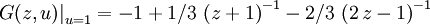 ,
,
así que el número de palabras es
De modo similar,
así que la suma de sus valores es
La conclusión es que el valor esperado es
El valor esperado es una palabra/número es lineal en el número de barras/peso del número.
La linearidad es evidente en el hecho de que la contribución de un dígito es un valor constante e independiente de su posición. Razonando con más cuidado, vemos que una palabra de peso n contiene como promedio 3 / 5n dígitos/letras, cuyo valor promedio es 17 / 3, dando un valor esperado aproximado de 17 / 5, lo cual no es lo bastante exacto, porque los dígitos no son equiprobables.
Material adicional en relación con este ejemplo, así como una instantánea de cómo se desarrolló, puede encontrarse en los «Enlaces externos«.
Enlaces externos
- Funciones generadoras, índices de potencias y cambio de moneda (en inglés) en Cut-the-knot.org (consultado el 1 de agosto de 2008)
- Versión descargable (PDF) en inglés de Generatingfunctionology, de H. Wilf (consultado el 1 de agosto de 2008)
- 1031 Generating Functions (consultado el 1 de agosto de 2008)
- Ignacio Larrosa Cañestro, León-Sotelo, Marko Riedel, Georges Zeller, Suma de números equilibrados, newsgroup es.ciencia.matemáticas
- Frederick Lecue; Riedel, Marko, et al., Permutation, Les-Mathematiques.net, en francés (el título desorienta un tanto)
- "Generating Functions" por Ed Pegg, Jr., en el sitio web The Wolfram Demonstrations Project, 2007. (consultado el 1 de agosto de 2008)
- León-Sotelo, José H. Nieto, Marko Riedel, et al., Alfa-barras, newsgroup es.ciencia.matemáticas
Categorías: Combinatoria | Exponenciales
Wikimedia foundation. 2010.

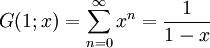
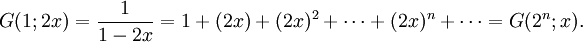
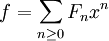
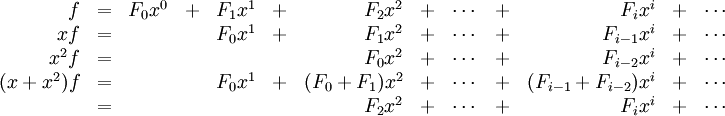
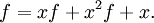

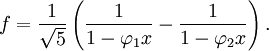

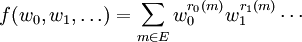
![c = [w_0^{r_0} w_1^{r_1} \cdots] f(w_0, w_1, \ldots),](/pictures/eswiki/57/9863003da933f52e4568ac6b20695433.png)
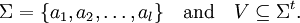

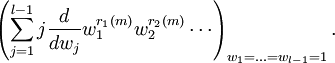
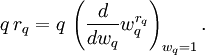

![v_k(q) = [z^q] \sum_{\lambda\in\Sigma} z^{|p_k(\lambda)|}.](/pictures/eswiki/99/c5aad7f46ed01ad70a4602c14e341ba9.png)
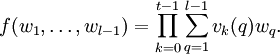
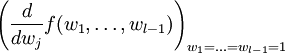
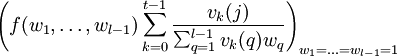
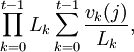
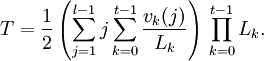

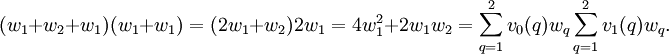
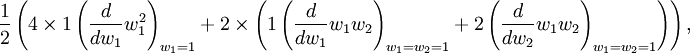
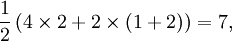
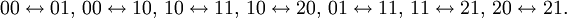
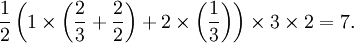
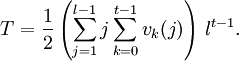
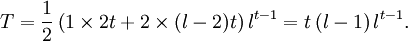

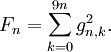
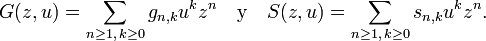
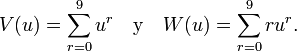
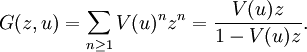
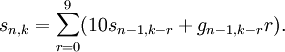

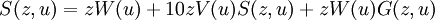
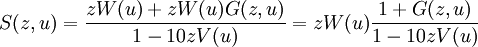
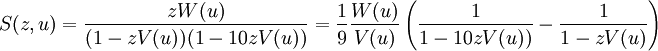
![E_n = \sum_{k=0}^{9 n} (10^n+1) [z^n u^k] S(z, u) \, [z^n u^k] G(z, u).](/pictures/eswiki/51/34c67e67df412c6d7172b075650ccc2d.png)

![E_n = (10^n+1) [u^{9n}] ([z^n] G(z, u) [z^n] S(z, u)).\,](/pictures/eswiki/98/be357beccb8ac5014f1af47a30d7db7e.png)
![[z^n] S(z, u) =
\frac{1}{9} \frac{W(u)}{V(u)}
\left( 10^n V(u)^n - V(u)^n \right) =
\frac{1}{9} W(u) (10^n - 1) V(u)^{n-1}](/pictures/eswiki/56/8d8149f319cdeda2395ffc61485b64f0.png)
![E_n = \frac{1}{9} (100^n - 1) [u^{9n}] W(u) V(u)^{2n-1}.](/pictures/eswiki/57/9262957a8f5888319d8a124a3ec407e9.png)
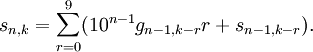
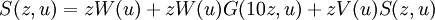
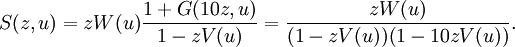
![[z^n] G(z, 1) = [z^n]\frac{10z}{1-10z} = 10^n,](/pictures/eswiki/49/14a264ebe8ce18e15e45b44f2143075b.png)
![[z^n] S(z, 1) = [z^n] \frac{45 z}{(1 - 10z)(1-100z)} =
[z^n] \left( \frac{1}{2} \frac{1}{1-100z} - \frac{1}{2} \frac{1}{1-10z} \right).](/pictures/eswiki/99/c4659f98c3ad07c7c68758bf55da0772.png)
![[z^n] S(z, 1) = \frac{1}{2} 100^n - \frac{1}{2} 10^n.](/pictures/eswiki/98/b2d427e77ddd888d5c15247dbd089fa3.png)
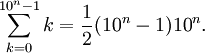
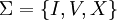
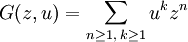
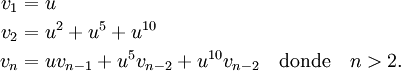
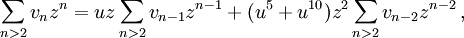
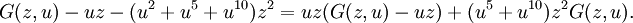
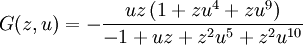
![E(n) =
\frac{ [z^n] \left. \frac{\operatorname{d}}{\operatorname{d}u} G(z, u) \right|_{u=1} }
{ [z^n] \left. G(z, u) \right|_{u=1} },](/pictures/eswiki/57/9bda7b842a2aee9892d67646fe1c6758.png)