Elemento irreducible en un dominio íntegro
- Elemento irreducible en un dominio íntegro
-
Elemento irreducible en un dominio íntegro
Wikimedia foundation.
2010.
Mira otros diccionarios:
Elemento irreducible en un dominio íntegro — En Teoría de Anillos, un elemento es irreducible si no puede descomponerse como el producto de dos elementos de manera que uno de ellos no sea una unidad … Enciclopedia Universal
Dominio de integridad — Saltar a navegación, búsqueda Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en… … Wikipedia Español
Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… … Wikipedia Español
Polinomio irreducible — Saltar a navegación, búsqueda En Teoría de Anillos, un polinomio no constante (y por lo tanto no nulo) p con coeficientes en un dominio íntegro R (es decir, ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos … Wikipedia Español
Elemento trascendente — Saltar a navegación, búsqueda La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos… … Wikipedia Español
Extensión simple — Saltar a navegación, búsqueda En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos L:K de manera que L está generado por un solo elemento. Contenido 1 Construcción 2 Definición de extensión simple … Wikipedia Español
Ideal (teoría de anillos) — En matemáticas, un ideal es una estructura algebraica definida en un anillo. Los ideales generalizan de manera fecunda el estudio de la divisibilidad en los números enteros. De este modo, es posible enunciar versiones muy generales de teoremas… … Wikipedia Español
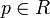 , siendo
, siendo 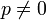 y
y 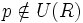 es un elemento irreducible en R si cuando ocurre que
es un elemento irreducible en R si cuando ocurre que 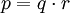 (con
(con 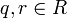 ) entonces también ha de ocurrir que
) entonces también ha de ocurrir que 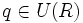 o que
o que 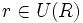 .Categoría: Teoría de anillos
.Categoría: Teoría de anillos