La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos coeficientes están en el cuerpo tiene sus raíces en el cuerpo (es decir, si al resolver la ecuación polinómica, las soluciones pertenecen o no al cuerpo).

Cuando un cuerpo está incluido en otro cuerpo puede ocurrir que los elementos del grande sean raíces de polinomios con coeficientes en el chico -en cuyo caso se dice que los elementos son algebraicos- o que haya elementos que no son raíces de ninguno de esos polinomios. En este último caso se dice que dichos elementos son trascendentes.

Construcción

(La siguiente información es de carácter técnico, y puede resultar ardua e incomprensible para el no iniciado en el Álgebra Abstracta, pero es esencial para comprender el desarrollo de esta rama de la Matemática. Por desgracia no puede exponerse de una manera más llana sin perder rigor, lo que haría que dejara de ser útil.)

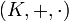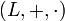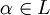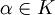Sean dos cuerpos y de forma que L es extensión de K. Sea . Si , entonces α es raíz del polinomio p(x) = x − α, que es irreducible en K[x] (todo polinomio de grado 1 es irreducible en cualquier anillo de polinomios). Si 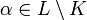, entonces realizamos la siguiente construcción:

• Construimos el conjunto . Este conjunto es un cuerpo, es extensión de K, es subcuerpo de L, y de hecho es la menor extensión de K que contiene a α. Se le denomina extensión generada por α sobre K.

• Construimos la aplicación que a cada polinomio le hace corresponder su evaluación en α, i.e., β(p) = p(α). Esta aplicación es de hecho un isomorfismo de anillos conmutativos y unitarios, y se denomina aplicación evaluación.

Ahora sólo pueden darse dos situaciones:

• Ker(β) = {0}, luego β es un monomorfismo. En ese caso, como , es β(a) = a para cada .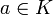

Por otra parte, β(x) = α. Sabemos, por la propiedad universal del cuerpo de cocientes de un dominio íntegro, que como β es monomorfismo, existe un monomorfismo 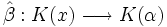de manera que 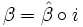, donde K(x) es el cuerpo de cocientes de K[x] e es el monomorfismo inclusión canónica (i.e., i(p) = p cualquiera que sea el ). Si 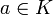, entonces 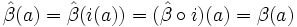, y 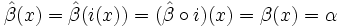. Así pues, 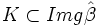y .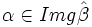

Por ser 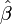homomorfismo entre cuerpos, es monomorfismo, luego 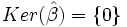. Por el Primer Teorema de Isomorfía, .

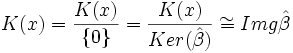Así pues, 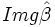es un subcuerpo de K(α), que contiene a K y a α. Como K(α) es la mínima extensión de K que contien a α e 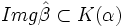, se concluye que 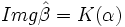, con lo que 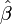es sobreyectiva, y como era monomorfismo, es isomorfismo.

Así, K(x) es isomorfo a K(α).

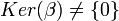• . Entonces se dice que α es un elemento algebraico.

En el primer caso (Ker(β) = {0}, o equivalentemente, 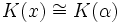) se dirá que el elemento α es trascendente sobre K y que K(α) es una extensión trascendente sobre K. En ese caso no existirá ningún polinomio con coeficientes en K que tenga por raíz a α (es decir, si , entonces ).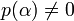

Véase también

Elemento algebraico

Número trascendente

Número algebraico

Extensión transcendente

Extensión algebraica