Elemento irreducible

Elemento irreducible

Elemento irreducible

En matemáticas, y más especialmente en teoria de anillos, una no-unidad en un dominio de integridad se dice que es irreducible si ésta no puede ser expresada como producto de dos no unidades. Equivalentemente, una no-unidad x es irreducible si x ≠ 0 y todo divisor d de x es un asociado de 1 o de x. Nótese que esta es la definición usual de número primo.

Todo elemento primo es irreducible. El recíproco es verdadero también para dominios de factorización única. Un ideal generado por un elemento primo es un ideal primo. Sin embargo, no es cierto en general que un ideal generado por un elemento irreducible sea un ideal irreducible.[1] Este es el caso en que A es un dominio MCD (en particular un DFU).[2]

Ejemplos

Los siguientes ejemplos muestran elementos irreducibles:

  • Polinomios irreducibles.
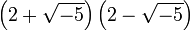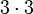  • En el anillo de enteros cuadráticos \mathbf{Z}[\sqrt{-5}], el número 3 es irreducible pero no es primo puesto que 9 puede ser escrito como \left(2 + \sqrt{-5}\right)\left(2 - \sqrt{-5}\right) y como 3\cdot 3.

Notas

  1. ↑ Así, en particular, no cualquier ideal primo es irreducible en general.
  2. ↑ http://planetmath.org/encyclopedia/IrreducibleIdeal.html
Obtenido de "Elemento irreducible"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Elemento irreducible en un dominio íntegro — Saltar a navegación, búsqueda En Teoría de Anillos, un elemento es irreducible si no puede descomponerse como el producto de dos elementos de manera que uno de ellos no sea una unidad. Definición. Sea R un dominio íntegro y U(R) el conjunto de… …   Wikipedia Español

  • Elemento irreducible en un dominio íntegro — En Teoría de Anillos, un elemento es irreducible si no puede descomponerse como el producto de dos elementos de manera que uno de ellos no sea una unidad …   Enciclopedia Universal

  • Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… …   Wikipedia Español

  • Elemento trascendente — Saltar a navegación, búsqueda La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos… …   Wikipedia Español

  • Polinomio irreducible — Saltar a navegación, búsqueda En Teoría de Anillos, un polinomio no constante (y por lo tanto no nulo) p con coeficientes en un dominio íntegro R (es decir, ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos …   Wikipedia Español

  • Dominio de integridad — Saltar a navegación, búsqueda Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en… …   Wikipedia Español

  • Anillo noetheriano — Saltar a navegación, búsqueda En álgebra, un anillo R es noetheriano por la izquierda si sus ideales por la izquierda satisfacen la condición de cadena ascendente. Diremos que un anillo es noetheriano si es noetheriano por la izquierda y por la… …   Wikipedia Español

  • Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una …   Wikipedia Español

  • Retículo (orden) — Diagrama de Hasse del retículo de particiones del conjunto {1,2,3,4}. En matemática, un retículo es una determinada estructura algebraica con dos operaciones binarias, o bien un conjunto parcialmente ordenado con ciertas propiedades específicas… …   Wikipedia Español

  • Cuerpo (matemática) — Saltar a navegación, búsqueda Para otros usos de este término, véase Cuerpo. Un cuerpo o campo es un anillo de división conmutativo, es decir, un anillo conmutativo en el que todo elemento distinto de cero (todo elemento no nulo) es invertible… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”