Polinomio irreducible

Polinomio irreducible

Polinomio irreducible

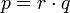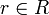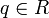En Teoría de Anillos, un polinomio no constante (y por lo tanto no nulo) p con coeficientes en un dominio íntegro R (es decir, p \in R[x]) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que deg(p). Es decir, si p = r \cdot q entonces ha de ser r \in R o q \in R (es decir, alguno de ellos ha de ser un polinomio constante).

Esto es un caso particular de elemento irreducible en un dominio íntegro.

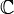El dominio íntegro R puede, entre otros, ser el conjunto \mathbb{R} de los números reales (que es dominio íntegro por ser cuerpo), el conjunto \mathbb{C} de los números complejos (también cuerpo), el conjunto 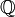\mathbb{Q} de los números racionales (cuerpo también) o el conjunto 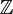\mathbb{Z} de los números enteros (que no es cuerpo pero sí dominio íntegro).


Ejemplos

Los cinco polinomios siguientes demuestran algunas características elementales de los polinomios reducibles e irreducibles:

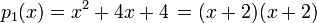p_1(x)=x^2+4x+4\,=(x+2)(x+2),
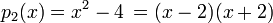p_2(x)=x^2-4\,=(x-2)(x+2),
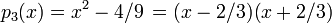p_3(x)=x^2-4/9\,=(x-2/3)(x+2/3),
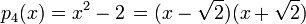p_4(x)=x^2-2\,=(x-\sqrt{2})(x+\sqrt{2}),
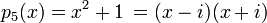p_5(x)=x^2+1\,=(x-i)(x+i).

Sobre el anillo 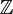\mathbb{Z} de números enteros, los primeros dos polinomios son reducibles, pero los tres últimos son irreducibles (el tercero no tiene coeficientes del número entero).

Sobre el cuerpo 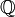\mathbb{Q} de números racionales, los primeros tres polinomios son reducibles, pero los otros dos son irreducibles.

Sobre el cuerpo \mathbb{R} de números reales, los primeros cuatro polinomios son reducibles, pero el quinto sigue siendo irreducible.

Sobre el cuerpo 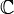\mathbb{C} de números complejos, los cinco polinomios son reducibles.

De hecho en 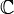\mathbb{C}, cada polinomio no-constante se puede descomponer en factores lineales

p(z)=a_n (z-z_1)(z-z_2)\cdots(z-z_n)

donde an es el coeficiente principal del polinomio y 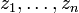z_1,\ldots,z_n son los ceros de p(x). Por lo tanto, todos los polinomios irreducibles son de grado 1.En el caso del cuerpo \mathbb{R}, tampoco pueden ser reducibles aquellos polinomios de grado 2 con discriminante negativo, ya que a pesar de ser factorizado por polinomios de menor grado que éste, y mayor o igual a 0, no tienen sus coeficientes dentro del cuerpo de los reales. Éste es el teorema fundamental del álgebra.


Un polinomio irreducible es polinomio primitivo si y solo si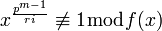 x^{{p^{m-1}}\over {ri}} \not \equiv 1 \bmod f(x)

p es primo

y x es un elemento de orden p^m \in \mathbb{Z}_p[x]/f(x)

Para probar si un polinomio es irreducible se pueden aplicar varios criterios, entre los que se encuentran el criterio de Eisenstein o el criterio de reducción.

Obtenido de "Polinomio irreducible"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Polinomio irreducible — En Teoría de Anillos, un no constante (y por lo tanto no nulo) con coeficientes en un dominio íntegro (es decir, ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que . Es decir,… …   Enciclopedia Universal

  • Polinomio primitivo — Saltar a navegación, búsqueda Un polinomio primitivo puede referirse a uno de los dos siguientes conceptos: Un polinomio sobre un dominio de factorización única (como el de los enteros) tal que el máximo común divisor de sus coeficientes es 1. El …   Wikipedia Español

  • Polinomio separable — Saltar a navegación, búsqueda En matemática, un polinomio P(X) es separable sobre un cuerpo K si sus raíces en una clausura algebraica de K son distintas es decir P(X) tiene factores lineales distintos en una extensión de cuerpo suficientemente… …   Wikipedia Español

  • Polinomio todo en uno — Saltar a navegación, búsqueda Un polinomio todo en uno (AOP, All in One Polynom) es un polinomio usado en campo finitos, especificalmente GF(2) (binario). El AOP es un 1 polinomio igualmente espaciado. Un AOP de grado m tiene todos los términos… …   Wikipedia Español

  • Polinomio mínimo — Saltar a navegación, búsqueda En matemática, el polinomio mínimo de un elemento α es el polinomio mónico p de menor grado tal que p(α)=0. Las propiedades del polinomio mínimo dependen de la estructura algebraica a la cual pertenece α. Teoría de… …   Wikipedia Español

  • Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… …   Wikipedia Español

  • Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una …   Wikipedia Español

  • Cuerpo finito — Saltar a navegación, búsqueda En álgebra abstracta, un cuerpo finito, campo finito o campo de Galois (llamado así por Évariste Galois) es un cuerpo que contiene un número finito de elementos. Los cuerpos finitos son importantes en teoría de… …   Wikipedia Español

  • Raíz de la unidad — Saltar a navegación, búsqueda En matemática, las raíces n ésimas de la unidad, o números de de Moivre, son todos los números complejos que resultan 1 cuando son elevados a una potencia dada n. Se puede demostrar que están localizados en el… …   Wikipedia Español

  • Transformación de Tschirnhaus — En matemáticas , una transformación de Tschirnhaus, desarrollado por Ehrenfried Walther von Tschirnhaus en 1683, es un tipo de asignación de polinomios . Puede definirse convenientemente por medio de la teoría del campo , como la transformación… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”