Extensión simple

Extensión simple: Extensión simple

Saltar a navegación, búsqueda

En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos $L : K$ de manera que L está generado por un solo elemento.

Contenido

1 Construcción

2 Definición de extensión simple

3 Observaciones

4 Teorema del elemento primitivo

Construcción

Sean $L$ y $K$ dos cuerpos de manera que $L$ es extensión de $K$ . Se define la extensión generada por $α$ sobre $K$ como el conjunto $K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x]\}$ .

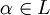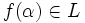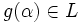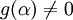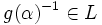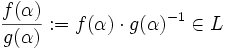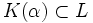Todo elemento de $K [x]$ está también en $L [x]$ , y como $\alpha \in L$ , si $f \in K[x]$ entonces $f(\alpha) \in L$ . Si $g \in K[x]$ entonces es $g(\alpha) \in L$ , y si $g(\alpha) \neq 0$ , existe $g(\alpha)^{-1} \in L$ . Así pues, $\frac{f(\alpha)}{g(\alpha)}:= f(\alpha) \cdot g(\alpha)^{-1} \in L$ y es $K(\alpha) \subset L$ .

Definimos las operaciones suma y producto en $K (α)$ como las restricciones a $K (α)$ de las operaciones del cuerpo de cocientes de $L$ , i.e., si 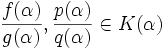$\frac{f(\alpha)}{g(\alpha)},\frac{p(\alpha)}{q(\alpha)} \in K(\alpha)$ , definimos 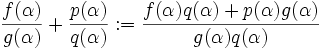$\frac{f(\alpha)}{g(\alpha)} + \frac{p(\alpha)}{q(\alpha)}:= \frac{f(\alpha)q(\alpha)+p(\alpha)g(\alpha)}{g(\alpha)q(\alpha)}$ y

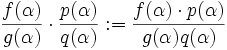$\frac{f(\alpha)}{g(\alpha)} \cdot \frac{p(\alpha)}{q(\alpha)} := \frac{f(\alpha)\cdot p(\alpha)}{g(\alpha)q(\alpha)}$ . Por ser $K [x]$ un anillo y $L$ un cuerpo, es sencillo demostrar que la suma y el producto así definidos en $K (α)$ son operaciones internas en $K (α)$ .

Como $L$ es cuerpo, en particular es dominio de integridad, y por la Propiedad Universal del Cuerpo de Cocientes de un Dominio Íntegro, el cuerpo de cocientes de $L$ es $Q (L) = L$ (el menor cuerpo que contiene a $L$ es el propio $L$ ). Así se demuestra que $K (α)$ , con las operaciones así definidas, es subcuerpo de $L$ .

Para comprobar que 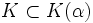$K \subset K(\alpha)$ , basta con tomar el cociente 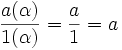$\frac{a(\alpha)}{1(\alpha)}=\frac{a}{1}=a$ para cada 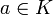$a \in K$ (donde identificamos 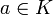$a \in K$ con el polinomio constante $a(x)=a \in K[x]$ ). Además, como las operaciones en $L$ son las extensiones de las operaciones en $K$ , es inmediato que $K$ es subcuerpo de $K (α)$ .

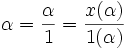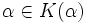Tomando el polinomio $x \in K[x]$ , entonces es $\alpha = \frac{\alpha}{1}=\frac{x(\alpha)}{1(\alpha)}$ , luego $\alpha \in K(\alpha)$ .

Todo esto demuestra que $K (α)$ es una extensión de $K$ y subcuerpo de $L$ .

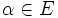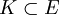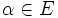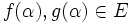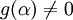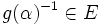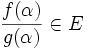Sea ahora una extensión $E$ de $K$ de forma que $\alpha \in E$ . Como $K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x]\}$ y $K \subset E$ , si $f,g \in K[x]$ , entonces $f,g \in E[x]$ , y como $\alpha \in E$ , entonces $f(\alpha), g(\alpha) \in E$ . 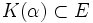Por último, como $E$ es cuerpo, si $g(\alpha) \neq 0$ , entonces existe $g(\alpha)^{-1} \in E$ y $\frac{f(\alpha)}{g(\alpha)} \in E$ , luego $K(\alpha) \subset E$ .

Queda entonces demostrado que $K (α)$ es la menor extensión de $K$ que contiene a $α$ .

A este proceso se le denomina a veces adjunción de un elemento $α$ a un cuerpo $K$ .

Definición de extensión simple

Sea $L : K$ una extensión. Se dice que $L$ es extensión simple sobre $K$ si existe un 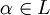$\alpha \in L$ de manera que $L = K (α)$ .

Observaciones

Una extensión simple $K (α) : K$ puede ser algebraica o trascendente, dependiendo de si $α$ es un elemento algebraico o trascendente sobre $K$ .

Si $α$ es trascendente, entonces el grado $[K (α) : K]$ de la extensión es infinito.

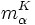Si $α$ es algebraico, entonces el grado $[K (α) : K]$ de la extensión es finito. En concreto, $[K(\alpha):K] = deg(m_{\alpha}^k)$ , siendo $m_{\alpha}^K$ el polinomio mónico irreducible de $α$ sobre $K$ . Se deduce que toda extensión simple que sea algebraica es de grado finito.

Teorema del elemento primitivo

Toda extensión finita y separable es simple.

Obtenido de "Extensi%C3%B3n simple"

Categorías: Wikipedia:Fusionar | Teoría de cuerpos

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Extension Simple — En mathématiques et plus précisément en algèbre dans le cas de la théorie de Galois, une extension de corps L d un corps K est dite simple si et seulement s il existe un élément l de L tel que L est égal à K[l]. Une extension simple est finie si… … Wikipédia en Français
Extension simple — En mathématiques et plus précisément en algèbre dans le cas de la théorie de Galois, une extension de corps L d un corps K est dite simple si et seulement s il existe un élément l de L tel que L est égal à K(l). Une extension simple est finie si… … Wikipédia en Français
Extensión simple — En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos de manera que L está generado por un solo elemento … Enciclopedia Universal
Extension De Galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français
Extension de galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français
Extension galoisienne — Extension de Galois En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de … Wikipédia en Français
Extension Algébrique — En mathématiques et plus particulièrement en algèbre, une extension algébrique L sur un corps K est une extension de corps dans laquelle tous les éléments sont algébriques sur K c’est à dire sont racines d un polynôme non nul à coefficients dans… … Wikipédia en Français
Extension algebrique — Extension algébrique En mathématiques et plus particulièrement en algèbre, une extension algébrique L sur un corps K est une extension de corps dans laquelle tous les éléments sont algébriques sur K c’est à dire sont racines d un polynôme non nul … Wikipédia en Français
Extension De Corps — En mathématiques, plus particulièrement en algèbre, l extension d un corps K est un corps L qui contient K comme sous corps. Par exemple, , le corps des nombres complexes, est une extension de , le corps des nombres réels, lequel est lui même un… … Wikipédia en Français
Extension Séparable — Une extension algébrique L d un corps K est dite séparable si et seulement si le polynôme minimal de tout élément de L n admet que des racines simples. Ce critère est une hypothèse nécessaire pour établir un théorème important de la théorie de… … Wikipédia en Français

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos