- Empaquetamiento compacto
-
Empaquetamiento compacto
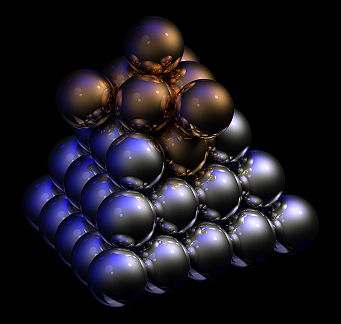
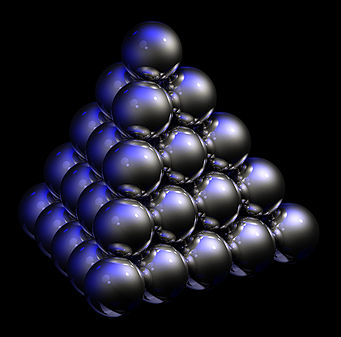Fig. 2 Fig. 2 Thomas Harriot aproximadamente en 1585 fue el primer matemático que calculó el número máximo de balas de cañón que pueden ser apiladas en forma de pirámide, con un empaquetamiento cúbico centrado en caras.. Adviertase cómo las dos bolas que quedan enfrente al observador en el segundo nivel de la figura superior contactan con la misma bola del nivel inferior. Esto no ocurre en un celosía HC (figura 1 a la izquierda, arriba, y figura 4, abajo).
Fig. 3 véase una forma modificada de la pila de balas de cañón en la que se han añadido tres esferas para mostrar totalmente las ocho esferas en los tres niveles superiores del empaquetamiento cúbico centrado en caras (diagrama de la fig. 1)
Fig. 4Fig. 4 Aquí se muestran las once esferas de la celda HC ilustrada en la Fig. 1. La diferencia entre esta pila y los tres niveles superiores de todas las pilas de balas de cañón se produce en la parte baja de nivel, que es la mitad de la rotación de distancia igual al diámetro de una esfera (60 °). Nota cómo las dos bolas del segundo nivel que quedan enfrente del espectador no contactan con las mismas bolas, en el nivel inferior.
Fig. 5 esta imagen animada ayuda a ilustrar las tres caras piramidales tetraedicas de las balas de cañor dispuestas como se muestra arriba en la figura 2.Empaquetamiento compacto de esferas es la disposición de un número infinito de celdas de esferas de forma que la mismas ocupen la mayor fracción posible de un espacio infinito tridimensional. Carl Friedrich Gauss demostró que la mayor densidad media que puede obtenerse con una disposición periódica es
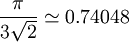. La Conjetura de Kepler establece que esta es la mayor que puede lograrse tanto para una disposición periódica como aperiódica.Existen dos reticulos periódicos que logran la mayor densidad media. Basándose en su simetría se denominan: empaquetamiento cúbico centrado en caras (CCC) y el empaquetamiento hexagonal compacto (HC).
Ambos se basan en la disposición de las esferas en los vértices de un triángulo telesctado; Se diferencian en la forma en que las celdas se apilan uno sobre otro. En ambos reticulos cada esfera tiene doce vecinos. En los dos casos hay un hueco rodeado por seis esferas (octaédricas) y dos pequeños huecos rodeados por cuatro esferas (tetraédrico).
En referencia a la disposición de una capa A, existen dos posible disposiciones B y C, Cada secuencia posible de A, B y C sin repeticiones da la misma densidad de empaquetamiento para las esferas de un radio dado.
Las más regulares son
- HC = ABABABA
- CCC = ABCABCA
En empaquetamiento compacto las líneas que unen los centros de las esferas en el plano x-y (visto desde arriba) forman una mosaico hexagonal, con una distancia entre los centros de las esferas igual a su diámetro, la distancia entre esferas paralelas en el eje z es
,
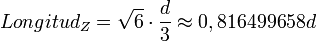donde d es el diámetro de la esfera; esto se deduce de la disposición tetraedrica del empaquetamiento compacto.
Muchas estructuras cristalinas están basadas en empaquetamientos compactos de átomos, iones, o grandes iones con otros más pequeños rellenando el espacio entre ellos. El empaquetamiento cúbico y el hexagonal están muy próximos entre si en cuanto a energía y es difícil predecir cual será la forma predilecta basándose en principios simples.
Contenido
Generación de reticulos
ps sta mooe shidooo`p su informe
Reticulo HC simple
Fig. 6 una animación de la generación de la celda HC.Véase también
Referencias
Enlaces externos
Categorías: Cristalografía | Geometría discreta
Wikimedia foundation. 2010.
