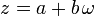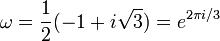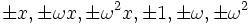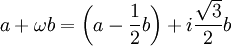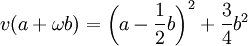Entero de Eisenstein

Entero de Eisenstein

Entero de Eisenstein

Enteros de Eisenstein como puntos de intersección de una retícula triangular en el plano complejo

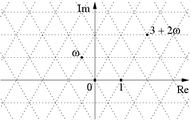
En matemáticas, los enteros de Eisenstein, llamados así por Ferdinand Eisenstein, son números complejos de la forma

z = a + b\,\omega

donde a y b son números enteros y

\omega = \frac{1}{2}(-1 + i\sqrt 3) = e^{2\pi i/3}

es una raíz cúbica de la unidad compleja.

Los enteros de Eisenstein forman un anillo conmutativo de enteros algebraicos en el campo de números algebraicos Q(√−3). También forman un dominio euclidiano.

Para ver que los enteros de Eisenstein son enteros algebraicos nótese que cada z = a + bω es una raíz del polinomio mónico

z2 − (2a − b)z + (a2 − ab + b2).

En particular, ω satisface la ecuación

ω2 + ω + 1 = 0.

Si x e y son enteros de Eisenstein, diremos que x divide a y si existe algún entero de Eisenstein z tal que

y = z x.

Esto extiende la noción de divisibilidad para los enteros ordinarios. Por lo tanto, podremos también extender la noción de primalidad; un entero de Eisenstein x será un primo de Eisenstein si sus únicos divisores son

\pm x, \pm\omega x, \pm\omega^2 x, \pm1, \pm\omega, \pm\omega^2

(excepto por que no consideraremos ±1, ±ω o ±ω² en sí mismos como primos de Eisenstein — son unidades en el anillo de los enteros.

Contenido

Relación con los primos de forma x² − xy + y²

Puede demostrarse que un primo de la forma x2 − xy + y2 puede ser factorizado en (x + ωy)(x + ω2y) y por lo tanto no es primo entre los enteros de Eisenstein. Nótese también que un número de la forma x² − xy + y² es primo si y solo si x + ωy es un primo de Eisenstein.


Dominio euclidiano

El anillo de los enteros de Eisenstein forma un dominio euclidiano cuya norma v es

v(a + ωb) = a2 − ab + b2.

Esto puede derivarse embebiendo los enteros de Eisenstein en los complejos: puesto que

v(a + ib) = a2 + b2

y puesto que

a + \omega b = \left( a - {1\over 2}b\right) + i {\sqrt{3}\over 2} b

se deduce que

v(a + \omega b) = \left( a - {1\over 2}b\right)^2 + {3\over 4} b^2
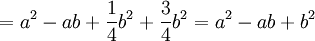= a^2 - a b + {1\over 4}b^2 + {3\over 4}b^2 = a^2 - a b + b^2.

Véase también

  • Primo de Eisenstein
  • Entero gaussiano
  • Anillo de Kummer

Enlaces externos

La versión inicial de este artículo es una adaptación de en:Eisenstein integer de Wikipedia en inglés.

Obtenido de "Entero de Eisenstein"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Entero de Eisenstein — En matemáticas, los enteros de Eisenstein, llamados así por Ferdinand Eisenstein, son números complejos de la forma donde a y b son números enteros y es una raíz cúbica de la unidad compleja …   Enciclopedia Universal

  • Entero cuadrático — En teoría de números, los enteros cuadráticos son una generalización de los enteros racionales a los cuerpos cuadráticos. Entre los ejemplos importantes se incluyen los enteros gaussianos y los enteros de Eisenstein. A pasar de que han sido… …   Wikipedia Español

  • Número primo de Eisenstein — En matemáticas, un primo de Eisenstein es un entero de Eisenstein aω + b que es irreducible (o equivalentemente primo) en el sentido de la teoría de anillos: sus únicos divisores de Eisenstein son las unidades 1, 1+ω, ω, 1, 1 ω, ω, y el propio aω …   Wikipedia Español

  • Número primo de Eisenstein — En matemáticas, un primo de Eisenstein es un entero de Eisenstein aω + b que es irreducible (o equivalentemente primo) en el sentido de la teoría de anillos: sus únicos divisores de Eisenstein son las unidades 1, 1+ω, ω, 1, 1 ω, ω, y el propio aω …   Enciclopedia Universal

  • Ferdinand Eisenstein — Saltar a navegación, búsqueda Ferdinand Gotthold Max Eisenstein (16 de abril de 1823 1 de octubre de 1852) fue un matemático alemán. Como Galois y Abel, Eisenstein murió antes de cumplir 30 años y, como Abel, su muerte se debió a la tuberculosis …   Wikipedia Español

  • Número entero algebraico — No debe confundirse con elemento algebraico. En teoría de números, un número entero algebraico es un número complejo que es la raíz de algún polinomio mónico (siendo el coeficiente principal 1) con coeficientes en ℤ. El conjunto de todos los… …   Wikipedia Español

  • Sergéi Eisenstein — Saltar a navegación, búsqueda Sergéi Eisenstein Nombre real Сергей Михайлович Эйзенштейн, Sergéi Mijáilovich Eizenshtéin (en letón: Sergejs Eizenšteins) Nacimiento 23 de enero de 1898 …   Wikipedia Español

  • Serguéi Eisenstein — Nombre real Serguéi Mijáilovich Eizenshtéin Nacimiento 23 de enero de 1898 …   Wikipedia Español

  • Criterio de Eisenstein — Saltar a navegación, búsqueda En matemática, el criterio de Eisenstein proporciona la condición suficiente para que un polinomio sea irreducible sobre Q (o, de forma equivalente, sobre Z). Si tenemos el siguiente polinomio con coeficientes… …   Wikipedia Español

  • Función divisor — σ0(n) representada hasta n=250. Función divis …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”