- Divisibilidad
-
Divisibilidad
Decimos que un número entero b es divisible entre otro entero a (distinto de cero) si existe un tercer entero c tal que:
b = a · c Se suele expresar de la forma a|b, que se lee a divide a b, o a es divisor de b, o también b es múltiplo de a. Por ejemplo, 6 es divisible por 3, ya que 6 = 3·2; pero no es divisible por 4, pues no existe un entero c tal que 6 = 4·c. Es decir, el resto de la división euclídea (entera) de 6 entre 4 no es cero. Véase el algoritmo de la división.
Todo número entero mayor que 1 es divisible por 1 y por sí mismo. Los números que no admiten más que estos dos divisores se denominan números primos. Los que admiten más de dos divisores se llaman números compuestos
Propiedades
Sean
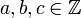 , es decir
, es decir 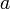 ,
, 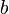 y
y  son números enteros. Tenemos las siguientes propiedades básicas:
son números enteros. Tenemos las siguientes propiedades básicas: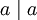 (Propiedad Refleja).
(Propiedad Refleja).- Si
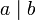 y
y 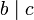 , entonces
, entonces 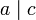 (Propiedad Transitiva).
(Propiedad Transitiva). - Si
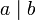 , entonces
, entonces 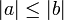 .
. - Si
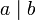 y
y 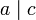 , entonces
, entonces 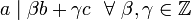 .
. - Si
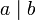 y
y 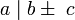 , entonces
, entonces 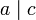
- Si
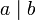 y
y 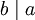 , entonces
, entonces 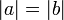 .
. - Si
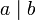 y
y 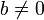 , entonces
, entonces 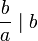 .
. - Para
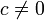 ,
, 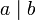 si y sólo si
si y sólo si 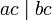
- Si
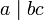 y
y 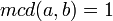 , entonces
, entonces 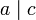 .
. - Si
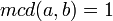 y
y  cumple que
cumple que 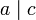 y
y 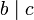 , entonces
, entonces 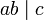 .
.
Como
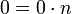 y
y  se tiene que
se tiene que 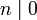 y
y 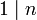 para todo
para todo 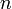 entero. Si
entero. Si 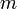 no es divisible por
no es divisible por 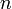 escribimos
escribimos 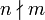 . Notemos que
. Notemos que 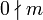 para todo
para todo 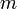 distinto de cero, pues
distinto de cero, pues 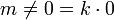 para todo
para todo 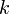 entero. .
entero. .Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división:
Véase también
- Tabla de divisores
- Máximo común divisor
Número Criterio Ejemplo 2 El número termina en cero o cifra par. 378: porque "8" es par. 3 La suma de sus cifras es un múltiplo de 3. 480: porque 4+ 8+ 0 = 12 es múltiplo de 3. 4 El número formado por las dos últimas cifras es 00 ó múltiplo de 4. 7324: porque 24 es múltiplo de 4. 5 La última cifra es 0 ó 5. 485: porque acaba en 5. 6 El número es divisible por 2 y por 3. 24: Ver criterios anteriores. 7 Para números de 3 cifras: Al número formado por las dos primeras cifras se le resta la última multiplicada por 2. Si el resultado es múltiplo de 7, el número original también lo es. 469: porque 46-(9*2)= 28 que es múltiplo de 7. Para números de más de 3 cifras: Dividir en grupos de 3 cifras y aplicar el criterio de arriba a cada grupo. Sumar y restar alternativamente el resultado obtenido en cada grupo y comprobar si el resultado final es un múltiplo de 7. 52176376: porque (37-12) - (17-12) + (5-4)= 25-5+1= 21 es múltiplo de 7. 8 El número formado por las tres últimas cifras es 000 ó múltiplo de 8. 27280: porque 280 es múltiplo de 8. 9 La suma de sus cifras es múltiplo de 9. 3744: porque 3+7+4+4= 18 es múltiplo de 9. 10 La última cifra es 0. 470: La última cifra es 0. 11 Sumando las cifras (del número) en posición impar por un lado y las de posición par por otro. Luego se resta el resultado de ambas sumas obtenidas. si el resultado es cero (0) o un múltiplo de 11, el número es divisible por éste. Si el número tiene dos cifras será multiplo de 11 si esas dos cifras son iguales.
42702: 4+7+2=13 · 2+0=2 · 13-2=11 → 11 es múltiplo de 11
44: porque las dos cifras son iguales.Entonces 44 es Múltiplo de 1112 El número es divisible por 3 y 4. 528: Ver criterios anteriores. 13 Para números de 3 cifras: Al número formado por las dos primeras cifras se le suma la última multiplicada por 4. Si el resultado es múltiplo de 13, el número original también lo es. 364: porque 36+4·4= 52 es múltiplo de 13. Para números de más de 3 cifras: Dividir en grupos de 3 cifras, sumar y restar alternativamente los grupos de derecha a izquierda y aplicar el criterio de arriba al resultado obtenido. Si es múltiplo de 13, el número original también lo es. 432549: porque 549-432 = 117 y luego 11 + 4·7 = 39 es múltiplo de 13. Categorías: Teoría de números | Aritmética elemental
Wikimedia foundation. 2010.
