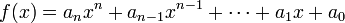En matemática, el criterio de Eisenstein proporciona la condición suficiente para que un polinomio sea irreducible sobre Q (o, de forma equivalente, sobre Z).

Si tenemos el siguiente polinomio con coeficientes enteros

y un número primo p tal que

• p divide a todo a_i para i ≠ n
• p no divide a a_n
• p² no divide a a₀

entonces f(x) es irreducible.

Ejemplos

Considérese g(x) = 3x⁴ + 15x² + 10.

Probaremos los siguientes primos p.

• p = 2

2 no divide a 15, entonces probaremos

• p = 3

3 no divide a 10, entonces probaremos

• p = 5

5 divide a 15, el coeficiente de x, y a 10, el término constante. Además, 5 no divide a 3, el primer coeficiente; y 25 = 5² no divide a 10. Concluiremos, por lo tanto, que g(x) es irreducible.

En algunos casos, la elección del primo puede ser poco clara, pero puede llegar a revelarse por un cambio de variable y = x + a. Por ejemplo, consideremos h(x) = x² + x + 2. Es aparentemente difícil, ya que ningún primo divide a 1, el coeficiente de x. Pero si cambiamos h(x) en h(x + 3) = x² + 7x + 14 veremos inmediatamente que el primo 7 divide al coeficiente de x y al término constante, y que 49 no divide a 14. Así, con el cambio introducido, logramos que el polinomio satisficiera el criterio de Eisenstein.

Otro caso notable es el del polinomio ciclotómico para un primo p. Esto es

(x^p − 1)/(x − 1) = x^{p − 1} + x^{p − 2} + ... + x + 1.

Aquí, el polinomio satisface el criterio de Eisenstein, en una nueva variable y, después de establecer x = y + 1. El coeficiente constante será entonces p; los otros coeficientes son divisibles por p por las propiedades de los coeficientes binomiales C(p,k) que son p! dividido por algo que no involucra a p.

Prueba elemental

Considérese f(x) como un polinomio módulo p; esto es, redúzcanse los coeficientes al cuerpo Z/pZ. Entonces será c.xⁿ para una constante c distinta de cero. Dado que dichos polinomios tienen una factorización única, cualquier factorización de f mod p resultará en monomios. Ahora, si f no fuese irreducible como polinomio entero, podríamos escribirlo como g.h, y f mod p como el producto de g mod p y h mod p. Estos últimos deben ser monomios, como acabamos de afirmar, por lo que tendremos que g mod p es d.x^k y h mod p es e.x^n-k donde c = d.e.

Vemos ahora que las condiciones dadas sobre g mod p y h mod p significan que p² dividirá a a₀, lo que contradice nuestra hipótesis. De hecho a₀ será g(0).h(0) y p divide a ambos factores, como hemos dicho más arriba.

Explicación avanzada

Aplicando la teoría del polígono de Newton para el campo de los números p-ádicos, para un polinomio de Eisenstein, se supone que tomaremos la menor envoltura convexa de los puntos

(0,1), (1, v₁), (2, v₂), ..., (n − 1, v_n-1), (n,0),

donde v_i es la evaluación p-ádica de a_i (es decir, la mayor potencia de p que lo divide). Ahora, los datos que tenemos sobre los v_i for 0 < i < n, es decir, que existe por lo menos uno, es lo que necesitamos para concluir que la menor envoltura convexa es exactamente el único segmento de (0,1) a (n,0), con pendiente −1/n.

De la teoría general sabemos que p se ramifica completamente en la extensión de los números p-ádicos generados por una raíz de f. Por esa razón, f es irreducible sobre el campo p-ádico, y a fortiori sobre el campo de los números racionales.

Esta prueba es mucho más complicada que el argumento directo por reducción módulo p. Sin embargo, permite ver, en términos de teoría algebraica de números, la frecuencia con que puede aplicarse el criterio de Eisenstein después de algún cambio de variable; y así limita marcadamente la posible elección de p.

De hecho sólo los primos p que se ramifiquen en la extensión de Q generada por una raíz de f tienen alguna posibilidad de servir. Pueden ser hallados en términos del discriminante de f. Por ejemplo, en el caso de x² + x + 2 dado más arriba, el discriminante es −7, de modo que 7 es el único primo con posibilidades de satisfacer el criterio. Se torna, mod 7, en

(x − 3)²

— es inevitable la repetición de una raíz, ya que el discriminante es 0 mod 7. Por lo tanto el cambio de variable es algo realmente predecible.

Una vez más, para el polinomio ciclotómico se torna en

(x − 1)^{p − 1} mod p;

Por métodos de álgebra lineal puede demostrarse que el discriminante es p^{p − 2} (excepto variación de signo).

La versión inicial de este artículo es una adaptación de en:Eisenstein's criterion de Wikipedia en inglés.