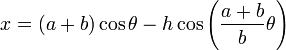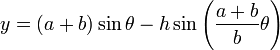- Epitrocoide
-
Epitrocoide
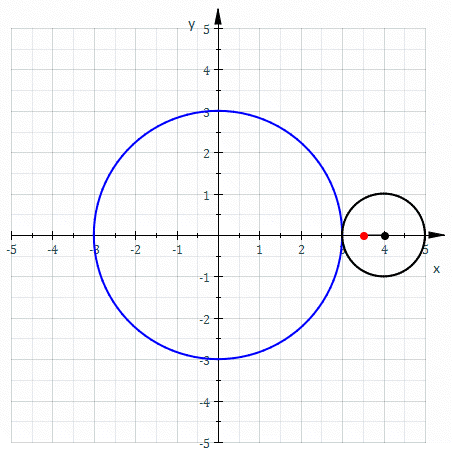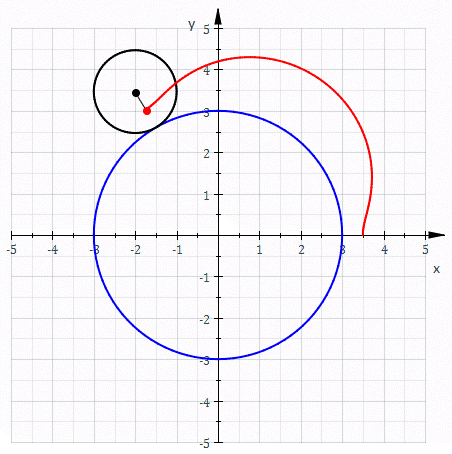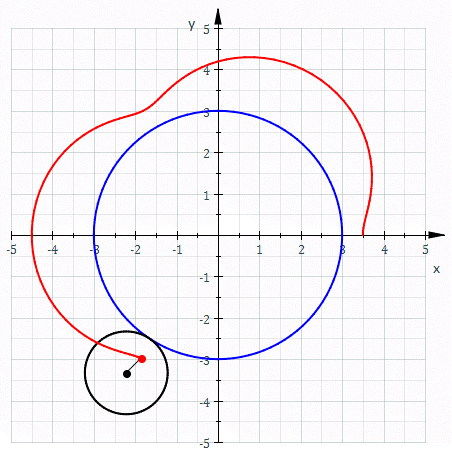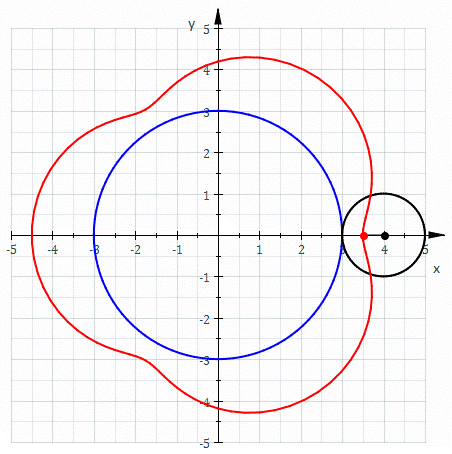 Epitrocoide (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: a = 3, b = 1 y h = 1/2
Epitrocoide (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: a = 3, b = 1 y h = 1/2
La epitrocoide, en geometría, es la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
Ecuaciones
Las ecuaciones paramétricas de una curva epitrocoide son:
donde a es el radio de la circunferencia directriz, b el radio de la circunferencia generatriz, y h la distancia del punto al centro de la circunferencia directriz.
Las epitrocoides son una clase general de curvas, entre las cuales encontramos el epicicloide (cuando h = b, es decir, cuando la curva queda determinada por un punto de la circunferencia generatriz) y el caracol de Pascal (cuando a = b, es decir, cuando los dos círculos tienen el mismo radio).
Son epitrocoides, por ejemplo, las órbitas de los planetas según la teoría geocéntrica de Ptolomeo, o el estátor del motor Wankel.
Véase también
Enlaces externos
- Weisstein, Eric W.. «Epitrochoid» (en inglés). Consultado el 18 de junio de 2008.
Categoría: Curvas
Wikimedia foundation. 2010.