Hipotrocoide

Hipotrocoide

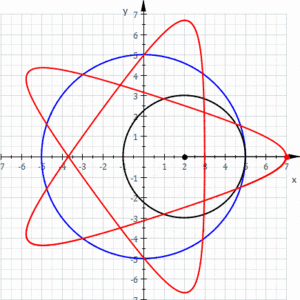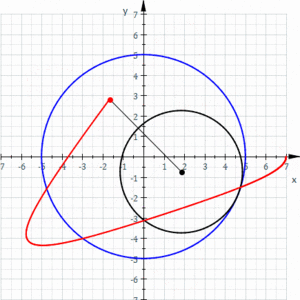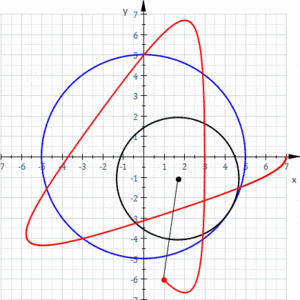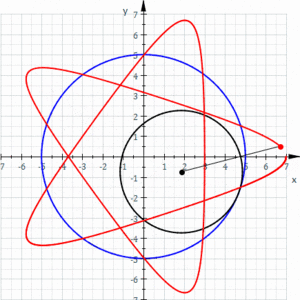
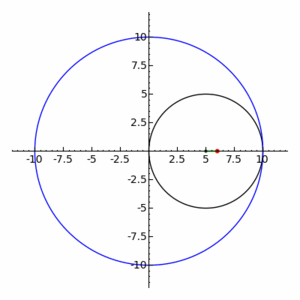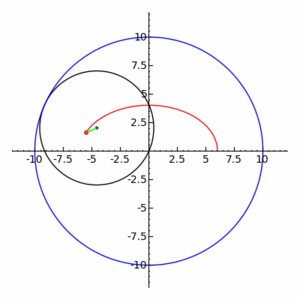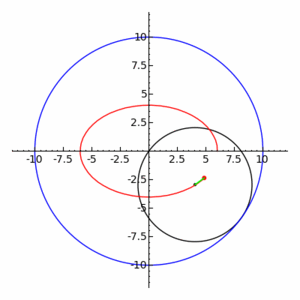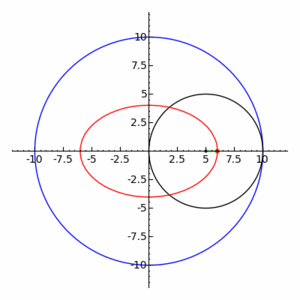
Una hipotrocoide, en geometría, es la curva plana que describe un punto vinculado a una circunferencia generatriz que rueda dentro de una circunferencia directriz, tangencialmente, sin deslizamiento.

La palabra se compone de las raíces griegas hipo hupo (abajo) y trokos (rueda).

Estas curvas fueron estudiadas por Albrecht Dürer en 1525, Ole Christensen Rømer en 1674 y Bernoulli en 1725.

Hipotrocoide (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: R = 5, r = 3, d = 5).
La elipse como caso particular de hipotrocoide. Parámetros: R = 10, r = 5 = R/2, d = 1.

Ecuaciones

Siendo q=\dfrac{a}{b} (donde q > 1) y d = kb, con circunferencia directriz de radio a, y circunferencia generatriz de radio b, y la distancia al centro de la generatriz d, la ecuación de la hipotrocoide es:

z = (a-b) e^{it} + d e^{-i(q-1)t} \,

donde:

qz = a[(q-1) e^{it} + k e^{-i(q-1)t}] \,
q(x + iy) = a(q − 1)cos(t) + ia(q − 1)sin(t) + akcos[(q − 1)t] − iaksin[(q − 1)t]

Por identificación de las partes reales e imaginarias se obtiene:

qx = a(q-1) \cos(t) + ka \cos[(q-1)t)]; \,
qy = a(q-1) \sin(t) - ka \sin[(q-1)t)]; \,

donde:

q = \dfrac{a}{b} y k=\dfrac{d}{b} \,.

Sabiendo que a = R, b = r y t = θ, obtenemos las ecuaciones siguientes:

x = (R - r)\cos\theta + d\cos\left({R - r \over r}\theta\right)
y = (R - r)\sin\theta - d\sin\left({R - r \over r}\theta\right)

el ángulo θ varía de 0 a 2π.

Las elipses son casos particulares de hipotrocoide, donde R = 2r.

Las hipocicloides son casos particulares, donde d = r (el punto fijo de la generatriz)

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Elipse — Saltar a navegación, búsqueda La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante positiva. Una elipse es la curva cerrada que resulta al cortar la… …   Wikipedia Español

  • Ruleta (geometría) — Saltar a navegación, búsqueda Ruleta, en matemática, se denomina a la curva plana que describe la trayectoria de un punto, vinculado a una curva generatriz C1, que rueda sobre otra curva directriz C2, tangencialmente, sin deslizamiento. Tanto C1… …   Wikipedia Español

  • Centered trochoid — In geometry, a centered trochoid is the roulette formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both… …   Wikipedia

  • Directriz — Saltar a navegación, búsqueda Una directriz[1] se dice de aquello que marca las condiciones en que se genera algo. En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea,… …   Wikipedia Español

  • Epitrocoide — Saltar a navegación, búsqueda Epitrocoide (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: a = 3, b = 1 y h = 1/2 La epitrocoide, en geometría, es la curva que describe un punto… …   Wikipedia Español

  • Generatriz — La generatriz[1] es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.[2] Si la generatriz es una línea recta que gira respecto de otra… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”