Escalas de tiempo estelares

Escalas de tiempo estelares

Escalas de tiempo estelares

Las estrellas son sistemas que permanecen estables durante la mayor parte de su vida. Pero los cambios de una fase a otra son etapas de transición que se rigen en escalas de tiempo mucho más cortas. A pesar de eso casi todas las escalas temporales superan con mucho a la humana. Las estrellas se hallan en un delicado equilibrio hidrostático entre la presión originada por las reacciones nucleares y la atracción gravitatorioria generada por toda su masa. La aceleración vertical neta del plasma que la compone habitualmente es casi nula por lo que casi siempre se dice que las estrellas están en condiciones cuasiestáticas. De hecho, vence la presión lo que conlleva ligeras pérdidas de masa en forma de viento solar, fulguraciones, eyecciones de masa coronal u otros fenómenos extrusivos. Pero para las estrellas de menos de 10 masas solares estas pérdidas son despreciables con respecto a su masa total.

Así pues podemos escribir una ecuación que iguale la presión producida por el movimiento radial del material estelar a la suma de las fuerzas de presión positiva (hacia afuera) generadas en el núcleo y las fuerzas negativas de la gravedad (hacia adentro).


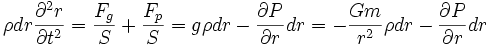
\rho dr \frac{\partial^2 r}{\partial t^2}=\frac{F_g}{S} + \frac{F_p}{S} = g \rho dr - \frac{\partial P}{\partial r}dr = -\frac{Gm}{r^2} \rho dr - \frac{\partial P}{\partial r}dr

Donde ρ (rho) es la densidad, r la distancia al centro, S la superficie y Fg la fuerza gravitatoria, Fp la fuerza de presión.

En las condiciones de equilibrio esta ecuación valdría aproximadamente cero ya que ambas fuerzas tenderían a igualarse.

Contenido

Escala de tiempo dinámica

En ocasiones se produce una gran descompensación entre presión y gravedad. Esto es así en los momentos finales de la vida de una estrella cuando las reacciones nucleares que sostienen a la estrella agotan su combustible y se vuelven incapaces de frenar el colapso. ¿A qué escala de tiempo se modificaría la estrella?

Para hacernos una idea de dicha escala de tiempo se usará la ecuación descrita en el apartado anterior. Si se anula la presión se hablará del coeficiente de caída libre si, en cambio, se elimina la componente de la gravedad se obtendrá una escala de tiempo explosiva. El hecho es que ambas escalas temporales son semejantes y se pueden denominar como escala de tiempo dinámica. Aislando y operando se obtiene:

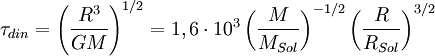\tau_{din} = \left ( \frac{R^3}{GM} \right )^{1/2} = 1,6 \cdot 10^3 \left ( \frac{M}{M_{Sol}} \right )^{-1/2} \left ( \frac{R}{R_{Sol}} \right )^{3/2} s.

Donde 1,6·10³ es el valor de G(-1/2) calculado en masas y radios solares.
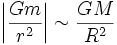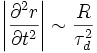
Así mismo, para hallar el resultado anterior se han realizado también las siguientes aproximaciones: \left | \frac{Gm}{r^2} \right | \sim \frac{GM}{R^2} y \left | \frac{\partial^2 r}{\partial t^2} \right | \sim \frac{R}{\tau^2_d}

Así, para el Sol el tiempo dinámico será de 1600 segundos, o sea, media hora aproximadamente. Como se ve si una de las dos fuerzas fallase los acontecimientos se sucederían muy repentinamente hasta volver a recuperar el equilibrio.

Nota: esta es la escala de tiempo a la que se transmiten las ondas sonoras u ondas de presión.

Escala de tiempo térmica

Mide cuanto tiempo puede subsistir la estrella con una determinada luminosidad a partir de sus reservas de energía potencial gravitatoria (Ω). Esta escala, por ejemplo, es la que rige la vida de las protoestrellas. Estos cuerpos ganan temperatura mediante el colapso gravitatorio hasta que llegan al punto de ignición del hidrógeno momento en el cual se transforman en estrellas de verdad.

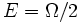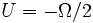En el equilibrio hidrostático se podrá hacer uso del Teorema del Virial según el cual: E=\Omega/2 \,\! y U=-\Omega/2 \,\! Donde E es la energía total, U la energía interna y Ω la energía potencial gravitatoria.

Así pues, cuando ocurre una contracción la mitad de la energía potencial liberada se transforma en energía interna que no es otra cosa que la agitación térmica. Esto hace aumentar la temperatura del interior. La otra mitad de la energía se libera en forma de radiación que contribuye a la luminosidad del astro.

En las estrellas, a medida que se agota una fase de combustión la luminosidad debería tender a disminuir pero esas pérdidas se van compensando con una contracción del núcleo. Este llega a calentarse tanto que llegado un punto empezará a quemar las cenizas de la fase anterior entrando en una segunda fase de combustión de helio. La realidad es que las estrellas no solo no pierden sino que, de hecho, ganan brillo con el paso del tiempo y esto es porque cada vez hay más material implicado en la fusión debido justamente a ese aumento de las temperaturas nucleares. De hecho, el propio núcleo no solo se contrae sino que aumenta su frontera englobando a nuevas capas de hidrógeno sin procesar.

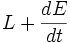
Se puede decir que mientras las estrellas pierden energía se calientan. La variación de la energía total de las estrellas es pues igual a la luminosidad. L+\frac{dE}{dt}

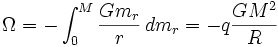
La energía potencial gravitatoria se calcula como: \Omega=-\int_{0}^{M}\frac{Gm_r}{r}\,dm_r=-q\frac{GM^2}{R}

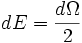
Sabiendo también que según el teorema del Virial: dE=\frac{d\Omega}{2}

A partir de estas tres relaciones se puede deducir la escala de tiempo térmica que da:

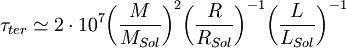\tau_{ter} \simeq 2 \cdot 10^7 {\left( \frac{M}{M_{Sol}} \right)}^2 {\left( \frac{R}{R_{Sol}} \right)}^{-1} {\left( \frac{L}{L_{Sol}} \right)}^{-1} a.

Para el Sol esto da unos 20 millones de años de tiempo térmico. Durante un tiempo esta fue la única hipótesis para el brillo del Sol y fue un gran misterio la discordancia entre la pequeña edad calculada para el sol frente a los registros geológicos y fósiles que databan de miles de millones de años atrás. Esto fue así hasta que se descubrió la energía nuclear.

Nota: esta es la escala de tiempo a la que se transmiten las ondas térmicas.

Escala de tiempo nuclear

Mide el tiempo que puede subsistir la estrella a partir de sus reservas de hidrógeno, helio o el combustible que esté quemando en ese momento. Para estudiarla basta con tratar básicamente la etapa del hidrógeno que es la que ocupa el 90% de la vida de las estrellas. Las estrellas son cuerpo formados en su mayor parte por hidrógeno y helio en menor medida. En el caso del Sol un 70% de este es hidrógeno. La mayoría de este hidrógeno no fusiona y solo en torno a un 10% acabará consumiéndose en el núcleo del común de las estrellas como el Sol. Si en el caso anterior el tiempo térmico era igual a la energía potencial gravitatoria dividida entre la luminosidad de la estrella aquí será lo mismo pero usando la energía nuclear obtenida a partir de las reacciones de fusión. Es decir:

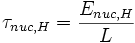
\tau_{nuc,H}=\frac{E_{nuc,H}}{L}

Donde: 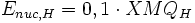E_{nuc,H}=0,1 \cdot XMQ_H Siendo X la fracción de masa de hidrógeno (0,7 en el caso del Sol), M la masa total y QH la energía liberada en la fusión de un gramo de hidrógeno. El coeficiente 0,1 se ha puesto asumiendo que solo un 10% de ese hidrógeno participará en las reacciones de fusión.

Sabiendo que QH = 6,3·1018erg/g y que en la secuencia principal la relación luminosidad masa es L α M3,5 se puede obtener el tiempo nuclear que será aproximadamente:

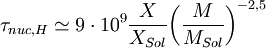\tau_{nuc,H} \simeq 9 \cdot 10^9 \frac {X}{X_{Sol}} { \left (\frac {M}{M_{Sol}} \right )}^{-2,5} a.

Para el Sol esto da unos 9 millardos de años de tiempo nuclear, que es un valor aproximado para la estancia del Sol en la secuencia pricipal.

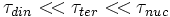Queda claro pues que: \tau_{din} <\!< \tau_{ter} <\!< \tau_{nuc} .

Bibliografía

  • Howard S. Goldberg: Physics of Stellar Evolution and Cosmology. M.E. Sharpe (1982). ISBN 0677055404
  • Amos Harpaz: Stellar Evolution. AK Peters, Ltd. (1994). ISBN 1568810121
  • Mike Inglis: Observer's Guide to Stellar Evolution. Springer (2003). ISBN 1852334657
  • Dina Prialnik: An Introduction to the Theory of Stellar Structure and Evolution. Cambridge University Press (2000). ISBN 052165937X
  • Robert T. Rood, Alvio Renzini, José Franco, Steven M. Kahn, Andrew R. King, Barry F. Madore: Advances in Stellar Evolution (Cambridge Contemporary Astrophysics). Cambridge University Press (1997). ISBN 0521591848

Véase también

Obtenido de "Escalas de tiempo estelares"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Evolución estelar — Saltar a navegación, búsqueda En astronomía, se denomina evolución estelar a la secuencia de cambios que una estrella experimenta a lo largo de su existencia. Durante mucho tiempo se pensó que las estrellas eran enormes bolas de fuego perpetuo.… …   Wikipedia Español

  • Estructura estelar — Saltar a navegación, búsqueda Esquema de una estrella. En una sección esférica cualquiera, la masa no experimenta expansiones ni contracciones, por lo que se considera un sistema cuasiestático. Así mismo su forma se aproxima bastante bien a la de …   Wikipedia Español

  • Estrella — Para otros usos de este término, véase Estrella (desambiguación). Las Pléyades, un cúmulo abierto de la constelación Tauro. En un sentido general, puede afirmarse que una estrella es todo objeto astronómico que brilla con luz propia.… …   Wikipedia Español

  • Formación estelar — Saltar a navegación, búsqueda Pilares de gas molecular en la nebulosa del águila. Algunas estrellas están aún formándose en su interior. La formación estelar es el proceso por el cual grandes masas de gas que se encuentran en galaxias formando… …   Wikipedia Español

  • Cuásar — Saltar a navegación, búsqueda Representación artística del cuásar GB1508 Un cuásar ó quásar (acrónimo en inglés de QUASi stellAR radio source) es una fuente astronómica de energía electromagnética, incluyendo radiofrecuencias …   Wikipedia Español

  • Enana roja — Saltar a navegación, búsqueda De acuerdo al diagrama de Hertzsprung Russell, una enana roja es una estrella pequeña y relativamente fría de la secuencia principal, ya sea de tipo espectral K tardío o M. Estas comprenden la vasta mayoría de las… …   Wikipedia Español

  • Wolf 359 — Constelación Leo Ascensión recta α 10h 56min 28,99s Declinación δ +07º 00’ 52,0’’ Distancia …   Wikipedia Español

  • Universo — Para otros usos de este término, véase Universo (desambiguación). La imagen de luz visible más profunda del cosmos, el Campo Ultra Profundo del Hubble. El universo es la totalidad del espacio y del tiempo, de todas las formas de la materia, la… …   Wikipedia Español

  • Sirio — Para otros usos de este término, véase Sirio (desambiguación). Sirio …   Wikipedia Español

  • Teoría del Big Bang — «Big Bang» redirige aquí. Para otras acepciones, véase Big Bang (desambiguación). Para la serie de televisión, véase The Big Bang Theory …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”