Esfera de Strömgren

Esfera de Strömgren: Esfera de Strömgren

Saltar a navegación, búsqueda

En astrofísica teórica, una esfera de Strömgren es una esfera de hidrógeno ionizado (H II) alrededor de una estrella joven de la case espectralO o B. Su contraparte en el mundo real son las regiones H II, un tipo de nebula de emisión, de la cual la más prominente es la nebulosa Rosetta. Fue descubierto por Bengt Strömgren en 1937 y luego nombrada en su honor.

Formula

El radio de Stromgren es el radio característico de una región HII, producida por el equilibrio de fotorrecombinación, para calcularlo sabemos que

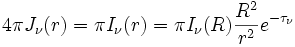
$4\pi J_{\nu}(r) = \pi I_{\nu}(r) = \pi I_{\nu}(R) \frac{R^2}{r^2} e^{-\tau_{\nu}}$

donde $π I ν (r)$ es el flujo de una fuente homogénea producida por un solo hemisferio (e.d. el flujo que se observa de la fuente, ignorando el flujo producido por la parte de "atrás" del emisor) a una distancia r, $I ν (R)$ es la energía producida a una distancia R, donde R es el Radio de la estrella y $τ ν$ es la profundidad óptica del medio.

Si observamos bien, la ecuación anterior nos dice que el promedio en energía a una distancia r es igual a la energía producida en la superficie de la fuente, multiplicada por el factor de decaimiento del flujo ( $R 2 / r 2$ ) y multiplicada por la absorción del gas.

Sustituyendo en la ecuación de equilibrio

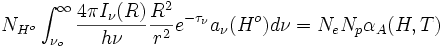
$N_{H^o}\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}\frac{R^2}{r^2} e^{-\tau_{\nu}}a_{\nu}(H^o)d\nu = N_eN_p\alpha_A(H,T)$

desarrollando y tomando la aproximación on-spot ( $α B = α A - α 1$ )

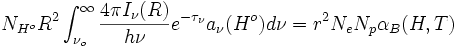
$N_{H^o}R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}e^{-\tau_{\nu}}a_{\nu}(H^o)d\nu = r^2N_eN_p\alpha_B(H,T)$

sabiendo que 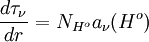$\frac{d\tau_{\nu}}{dr} = N_{H^o}a_{\nu}(H^o)$ entonces 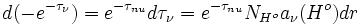$d(-e^{-\tau_{\nu}}) = e^{-\tau_{nu}}d\tau_{\nu} = e^{-\tau_{nu}}N_{H^o}a_{\nu}(H^o)dr$ Si sustituimos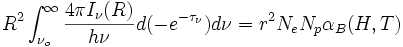

$R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}d(-e^{-\tau_{\nu}})d\nu = r^2N_eN_p\alpha_B(H,T)$

integrando sobre r

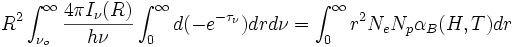
$R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}\int_0^{\infty}d(-e^{-\tau_{\nu}})drd\nu = \int_0^{\infty}r^2N_eN_p\alpha_B(H,T)dr$

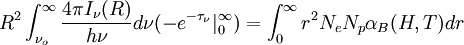
$R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}d\nu (-e^{-\tau_{\nu}}|_0^{\infty}) = \int_0^{\infty}r^2N_eN_p\alpha_B(H,T)dr$

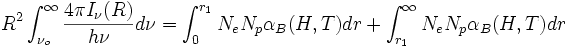
Si suponemos que a una distancia $r 1$ todo se encuentra ionizado, entonces $N e = N p = N H$ y después de esa region $N e = 0$ entonces $R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}d\nu = \int_0^{r_1}N_eN_p\alpha_B(H,T)dr + \int_{r_1}^{\infty}N_eN_p\alpha_B(H,T)dr$

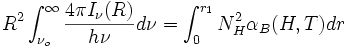
$R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}d\nu = \int_0^{r_1}N_H^2\alpha_B(H,T)dr$

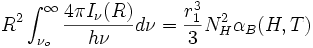
$R^2\int_{\nu_o}^{\infty}\frac{4\pi I_{\nu}(R)}{h\nu}d\nu = \frac{r_1^3}{3}N_H^2\alpha_B(H,T)$

Como

$L ν = 4π R 2 π I ν (R)$

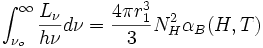
$\int_{\nu_o}^{\infty}\frac{L_{\nu}}{h\nu}d\nu = \frac{4\pi r_1^3}{3}N_H^2\alpha_B(H,T)$

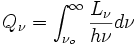
sustituyendo $Q_{\nu} = \int_{\nu_o}^{\infty}\frac{L_{\nu}}{h\nu}d\nu$

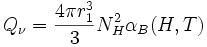
llegamos $Q_{\nu} = \frac{4\pi r_1^3}{3}N_H^2\alpha_B(H,T)$

donde $r 1$ es el radio de Stromgren para una región solo de Hidrógeno.

Enlaces externos

Calcular el radio de Stromgren

Obtenido de "Esfera de Str%C3%B6mgren"

Categoría: Astrofísica